Kalman 滤波器节拍跟踪的 Matlab 仿真研究

Y. Shiu, N. Cho, P. -C. Chang and C. . -C. J. Kuo, “Robust on-line beat tracking with kalman filtering and probabilistic data association (KF-PDA),” in IEEE Transactions on Consumer Electronics, vol. 54, no. 3, pp. 1369-1377, August 2008, doi: 10.1109/TCE.2008.4637629.

摘要

搭建了 Kalman 滤波在线跟踪系统 Source Code，使用 Matlab 内置音频工具箱 AudioToolbox 可从文件或者设备读取音频流，放进 Buffer 内做重音（Onset）检测，作为卡尔曼滤波器的输入，得到下一拍的估计，实现了在线（实时）的节拍跟踪。拍位置的观测方法为局部最大值规则（LM），不过丢拍、错拍概率比较高，但还未统计正确率和最长持续跟踪时间。目前尝试PDA算法选取观测拍，但是统计重音强度分布时遇到了问题。

主文件为beattrack.m, 运行之前需要设置音频I/O设备或者文件路径。

音频流 I/O 函数

使用matlab内置音频工具箱AudioToolbox的函数实现
dsp.AudioFileReader | dsp.AudioFileWriter | audioDeviceReader | audioDeviceWriter
具体参考官方手册: Audio I/O: Buffering, Latency, and Throughput.

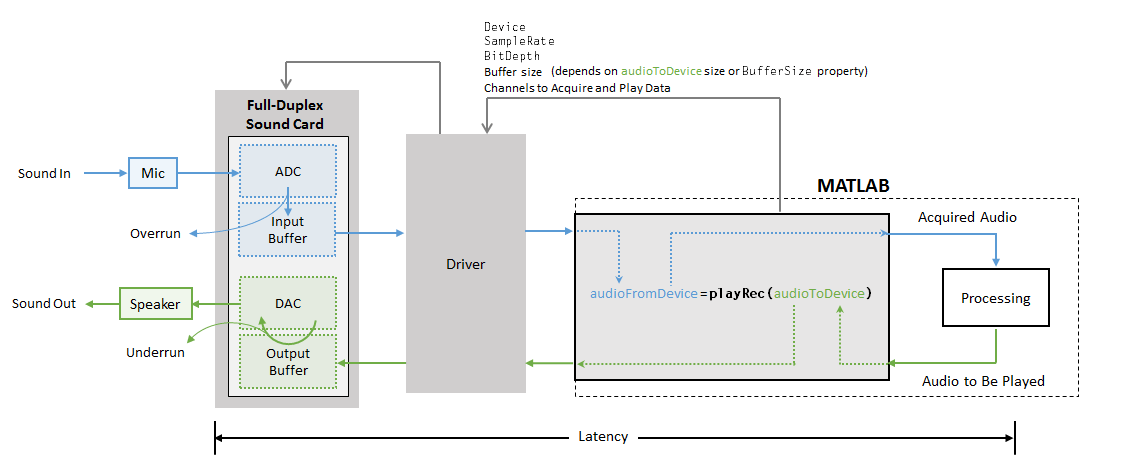
streamprocessing3

需要设置的参数有一次采样率 sr ，读取的音频长度 readtime ，输入、输出 Device / Filename，Device 可以使用 getAudioDevices获取。
注意: 同时拾音和收音需要考虑音频串流的问题，目前在MAC上可以用虚拟声卡软件「Loopback」提取音轨，Windows系统上还没找到比较好的解决方案。

添加一个处理Buffer

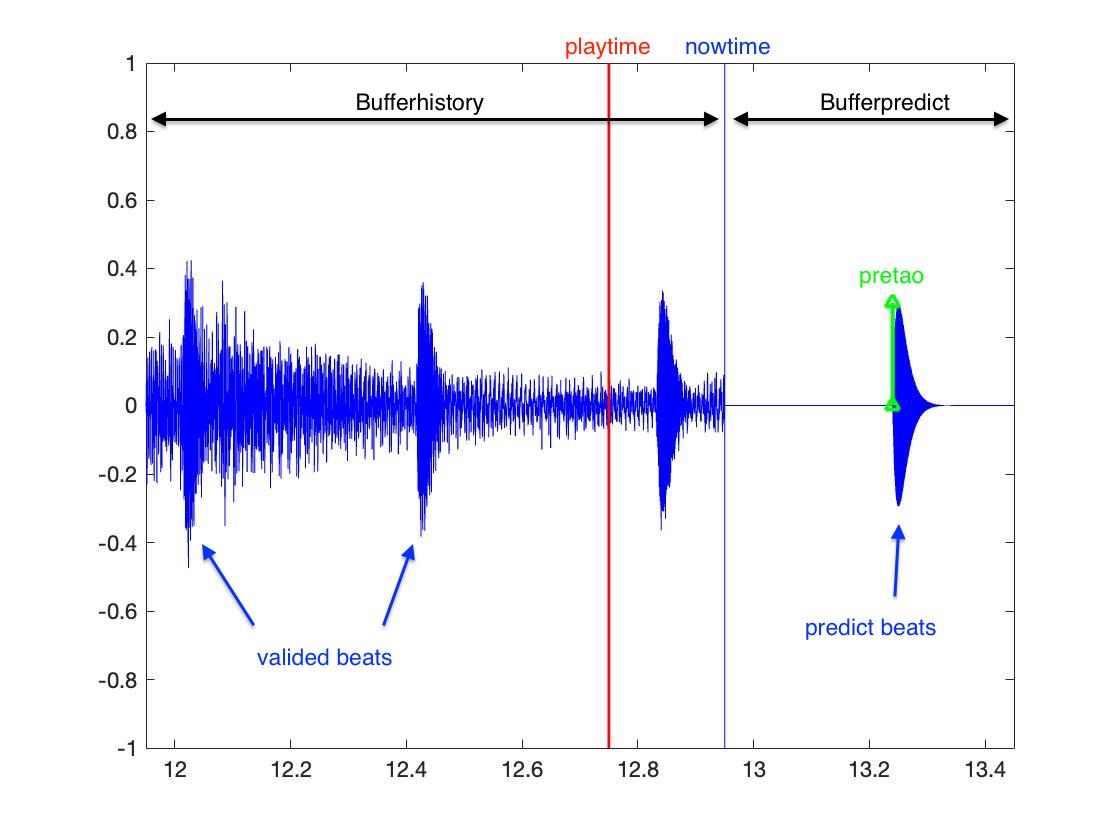
由于“音频读取–处理–估计–播放”循环存在延迟，因此验证拍永远落后于实际音频播放的时间。设置一个处理Buffer，长度由历史缓存bufferhistory和预估缓存bufferpredict构成。历史缓存bufferhistory用于重音观测，预估缓存bufferpredict用于放置和播放预估得到的拍子。

Buffer随着歌曲进行向前推移，可与通过卡尔曼滤波或自相关运算获得的预估拍，再经LM观测得到新的验证拍，如此递归运算。

realtime

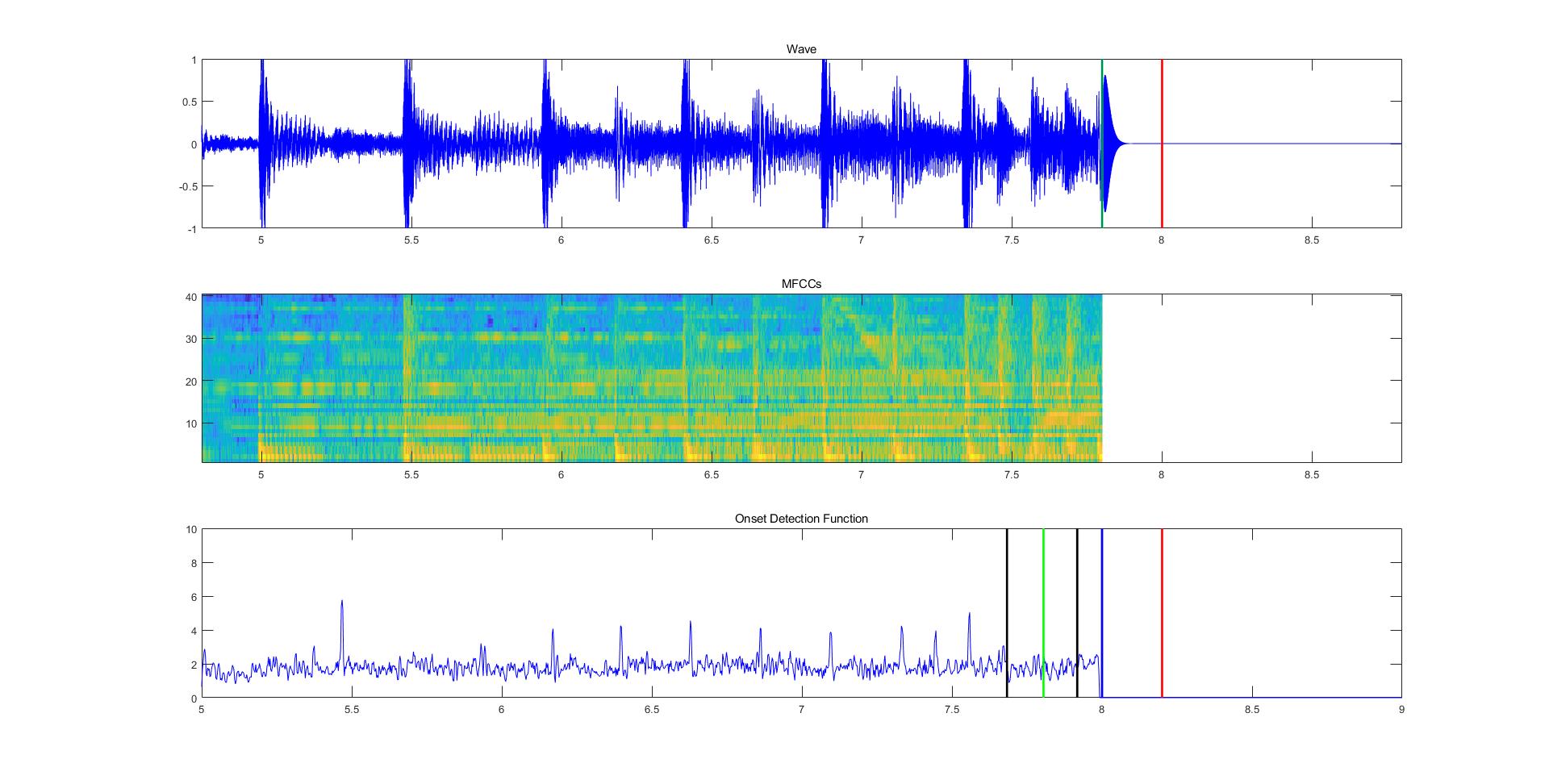
使用`tempo()`计算重音检测函数

tempo() 是 coversongID 库给出的预处理函数，功能有：计算梅尔频谱 D、给出重音检测函数 onsetenv、检测函数的自相关运算 xcr，以及根据自相关运算结果给出2个候选速度 startpd, startpd2。

tempo() 给出的 onsetenv 经过dc-remove滤波，去掉这个filter以后,增加了 p=3 的均值滤波，得到正常的重音检测函数 df。在Buffer内绘制出 df ,观测后发现主要是存在休止符和非节拍Onsets干扰的问题，导致卡尔曼滤波效果不稳定。

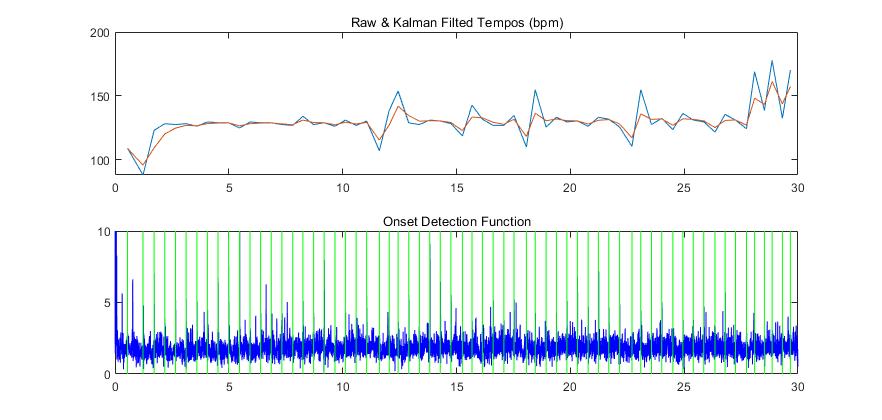
最后添加了整首歌曲在Kalman滤波前、后的节拍周期 obvtempos, filttempos 的对比曲线。

局部最大值规则（$LM$）

局部最大值规则的数学描述为

\[\tau_{k} = \underset{\left|n-\hat{\tau}_{k \mid k-1}\right|<W / 2}{\arg \max } d(n)\]

其中 $\tau_{k}$ 第 $k$ 步的拍子位置, $W$ 是一个固定长度的窗口。于是预测的拍子位置为

\[\hat{\tau}_{k \mid k-1}=\hat{\tau}_{k-1 \mid k-1}+\hat{\Delta}_{k-1 \mid k-1}\]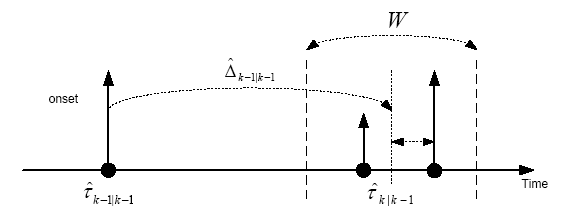

model

给定观测窗口位置是预估拍 pretao ，窗口宽度 w 可选取为20%预估节拍周期长度 0.2*predelta，于是，当 nowtime 超过 pretao + w/2 时进行一次 $LM$，得到的拍子位置观测值 obvtao 放入卡尔曼滤波进行估计。

卡尔曼滤波器

将节拍进行描述为一个动态线性系统，其具有两个状态变量拍子位置 $\tau$ 周期 $\hat{\Delta}$. 则第 $k$ 步状态变量描述为

\[\mathbf{x}_{k}=\left[\hat{\tau}_{k}, \hat{\Delta}_{k}\right]^{T}\]

卡尔曼滤波预测阶段为：

\[\begin{aligned} &\hat{\mathbf{x}}_{k \mid k-1}=\boldsymbol{\Phi}_{k} \hat{\mathbf{x}}_{k-1 \mid k-1} \\ &\mathbf{P}_{k \mid k-1}=\boldsymbol{\Phi}_{k} \mathbf{P}_{k-1 \mid k-1} \boldsymbol{\Phi}_{k}^{\mathrm{T}}+\mathbf{Q}_{k-1} \end{aligned}\]

其中 $\boldsymbol{\Phi}_{k} = \left[\begin{array}{ll}1 & 1 \\ 0 & 1\end{array}\right]$；$\hat{\mathbf{x}}_{k \mid k-1}$ 和 $\mathbf{P}_{k \mid k-1}$ 分别表示预测状态和协方差；过程噪声 $\mathbf{w}_{k} \sim N\left(\mathbf{0}, \mathbf{Q}_{k}\right)$；

卡尔曼滤波更新阶段为：

\[\begin{aligned} \mathbf{K}_{k} &=\mathbf{P}_{k \mid k-1} \mathbf{M}_{k}^{\mathrm{T}}\left(\mathbf{M}_{k} \mathbf{P}_{k \mid k-1} \mathbf{M}_{k}^{\mathrm{T}}+\mathbf{R}_{k}\right)^{-1} \\ \hat{\mathbf{x}}_{k \mid k} &=\hat{\mathbf{x}}_{k \mid k-1}+\mathbf{K}_{k}\left(\mathbf{y}_{k}-\mathbf{M}_{k} \hat{\mathbf{x}}_{k \mid k-1}\right) \\ \mathbf{P}_{k \mid k} &=\left(\mathbf{I}-\mathbf{K}_{k} \mathbf{M}_{k}\right) \mathbf{P}_{k \mid k-1} \end{aligned}\]

其中 $\mathbf{K}_{k}$ 是卡尔曼增益；

$\hat{\mathbf{x}}_{k \mid k}$ 和 $\mathbf{P}_{k \mid k}$ 分别表示第 $k$ 步滤波得到的状态和协方差；

$\mathbf{M}_{k}=\left[\begin{array}{ll}1 & 0\end{array}\right]$,

$\mathbf{R}_k$ 为观测噪声的方差；

$ \mathbf{y}_k$ 是观测值。

上述过程Matlab实现如下：给定拍子位置 tao 和节拍周期 delta 以及对应的协方差 P，并加入过程噪声 Q 和观测噪声 R ,于是卡尔曼滤波器实现如下：

% % % KalmanFilter.m % % %
% Predict
xp = A * x;
Pp = A * P * A' + Q;

% Update
K = Pp * M' / ( M * Pp * M' + R);
x = xp + K * (y - M * xp);
P = Pp - K * M * Pp;   

可选择的播放位置

我们可以选择播放Buffer内任意位置的音频，通过一个延迟参数 playdelay 来实现，其含义为播放时间playtime 是当前时间 nowtime 延迟 playdelay 秒。如果 playdelay 设置为大于 w ，则播放的为已验证的拍和音乐，如果 playdelay 小于0, 则播放的是预估的拍子，但没有音乐，其中 w 是验证窗口，长度为20%～30%的节拍周期。如果在 w 验证窗口内播放，可能会同时听到估计拍和观测拍的声音。

利用 playdelay 可以提前将预估拍子播放出来，抵消掉音频处理系统的“音频读取–处理–估计–播放”循环的延迟，实现在线节拍跟踪，提前的时间可能需要根据不同的处理系统具体测量，目前根据效果手动指定为0.2s。

wave

概率数据关联(PDA)

PDA算法用概率的方法同时讨论所有观测到的候选拍。理想情况下，PDA能拾取所有目标观测值，并丢弃随机噪声和干扰引起的其他测量值。

PDA算法分为两步：

一、验证测量值：限制了测量值选取的范围，减少候选拍。给定阈值系数 $\gamma$, 拍子位置方差 $p_{11}$和观测噪声方差 $\sigma_v^2$，则第k步的观测验证区域可以写成：

\[\hat{\mathbf{y}}_{k \mid k-1}-\gamma\left(p_{11}+\sigma_{v}^{2}\right) \leq \mathbf{y} \leq \hat{\mathbf{y}}_{k \mid k-1}+\gamma\left(p_{11}+\sigma_{v}^{2}\right)\]

当 $\gamma$ = 9 时验证区域内包含测量真值的可能性为 99.7%, 当 $\gamma$ = 4 时为 95.4%.

确定验证区域后，下一步是进行概率数据关联（或叫概率数据加权）。每一次采样时，都会计算一次测量验证空间，如果落入测量空间的候选测量值不止一个，那么就对所有候选测量值进行PDA。

二、关联测量值(PDA)：将候选的测量值与目标通过概率关联起来，获得一个更准确的测量值。

1、确定权重系数

人类确定拍子位置的依据有重音强度和位置，遂同时引入重音强度和预测残差提升节拍跟踪的效果。权重 $\beta_{i}(k)$ 也被称为关联概率, 与候选拍和预测拍之间距离 (预测残差) 有关, 距离越近，重音强度越高，概率越大。

\[\begin{aligned} \beta_{i}(k) &=p\left[\theta_{i}(k) \mid I_{Y}(k), \mathbf{Y}^{k}\right] \\ & \propto p\left[I_{Y}(k) \mid \theta_{i}(k), \mathbf{Y}^{k}\right] p\left[\theta_{i}(k) \mid \mathbf{Y}^{k}\right] \end{aligned}\]

其中 $I_{Y}(\cdot)$ 是重音持续时间的分布函数；$\beta_{i}(k)$ 第一项由候选拍的重音强度贡献，第二项由候选拍的位置误差贡献。由文献[11]，第一项可以写为

\[p\left[I_{Y}(k) \mid \theta_{i}(k), \mathbf{Y}^{k}\right]=I_{i}\left(\mathbf{y}_{i}\right) \prod_{j=1, j \neq i}^{m_{k}} I_{0}\left(\mathbf{y}_{j}\right)\]

其中, $I_{i}\left(\mathbf{y}_{i}\right), i=1, \cdots, m_{k}$ 是验证观测值 $y_{i}$ 的概率分布；$I_{0}\left(\mathbf{y}_{j}\right)$ 是观测值 $y_{j}$ 不在验证空间内的概率分布

但是, 验证观测值 $\mathrm{y}_{\mathrm{i}}$ 的概率分布 $I_{i}\left(\mathbf{y}_{i}\right), i=1, \cdots, m_{k}$ : 难以快速准确地确定。

因此，使用一个固定概率分布 $I_{B}$ 来替代 $I_{i}(k)$, 此概率分布即为重音强度关于节拍位置的概率分布;使用概率分布 $I_{N}$ 来替代 $I_{0}(k)$, 此概率分布即为重音强度关于非节拍位置的概率分布。这两个固定概率分布通过统计的方法来估计。

利用MIREX数据集里20个音乐片段的前10s计算$I_B$和$I_N$, 绘出关于重音强度的直方图如图(Beat对应$I_B$，Non-Beat对应$I_N$)：

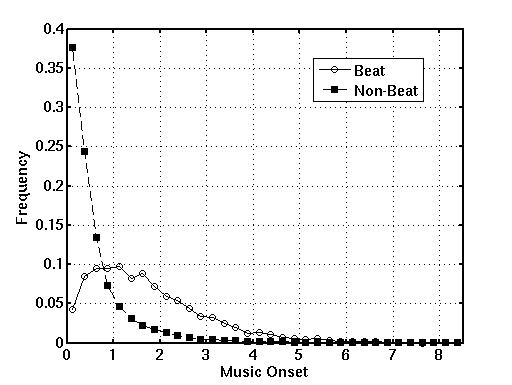
intensity in paper

可以得到一个基本结论：非节拍重音集中分布于较短的重音持续时间上。

假设候选拍的位置服从高斯分布，则第二项可以写为

\[p\left[\mathbf{y}_{k} \mid \mathbf{Y}^{k-1}\right]=N\left(\hat{\mathbf{y}}_{k \mid k-1}, \mathbf{S}_{k}\right)\]

其中，预测观测值 $\hat{\mathbf{y}}_{k \mid k-1}=\mathbf{M}_{k} \hat{\mathbf{x}}_{k \mid k-1}$；

相关协方差矩阵 $\mathbf{S}_{k}=\mathbf{M}_{k} \mathbf{P}_{k \mid k-1} \mathbf{M}_{k}^{\mathbf{T}}+\mathbf{R}_{k}$

在Matlab里，权值系数bta计算方式如下：

假设验证区域中有多个候选拍，对于其中某个候选拍k为真实拍的概率可以分两部分计算。
No.1 一如卡尔曼滤波器假设，估计拍的分布是一个均值估计位置pretao,方差P(1,1)的高斯分布

pdf = normpdf(window, pretao, sqrt(P(1,1)))

则某一候选拍为真实拍的的概率就是其位置在此高斯分布上的位置概率ploc，显然ploc与测量残差相关。

No.2 使用已标注的数据集，统计检测函数上重音强度(Beat Intensity)和非重音强度(Non-Beat Intensity)的概率分布，则根据候选拍的重音强度可以在分布上取得其为真实拍的概率pb,和其他候选拍不是真实拍的概率值pn1, pn2… 于是该候选拍的强度概率pints为

pints = pb·pn1·pn2...

综合上述两项概率，则该候选拍为真实拍的概率为：

pk = ploc * pints;

那么所有候选拍的概率可以确定了，这就是他们的权值bta, 再根据贝叶斯概率公式计算出所有候选拍都不是真实拍的概率bta0：

bta0 = 1 - prod(1-bta);

2、概率数据加权

PDA将状态估计分解为候选观测值的线性组合， $\begin{aligned} \hat{\mathbf{x}}_{k \mid k} &=E\left[\mathbf{x}_{k} \mid \mathbf{Y}^{k}\right] \\ &=\sum_{i=0}^{m_{k}} E\left[\mathbf{x}_{k} \mid \theta_{i}(k), \mathbf{Y}^{k}\right] p\left[\theta_{i}(k) \mid \mathbf{Y}^{k}\right] \\ &=\sum_{i=0}^{m_{k}} \hat{\mathbf{x}}_{i, k \mid k} \beta_{i}(k), \end{aligned}$

其中,

$m_{k}$ 是已验证候选拍的数量;

$\hat{\mathbf{x}}_{i, k \mid k}$ 是以事件 $\theta_{i}(k)$ 为条件的更新得到的状态估计;

$\theta_{i}(k)$ 表示观测到的 $\hat{\mathbf{y}}_{i, k}$ 来自于目标拍;

$\theta_{0}(k)$ 表示没有观测来自于目标拍;

$\beta_{i}(k)$ 表示事件 $\theta_{i}(k)$ 发生的概率, 即

\[\beta_{i}(k)=p\left[\theta_{i}(k) \mid \mathbf{Y}^{k}\right], i=0, \cdots, m_{k}\]

且 $\sum_{i=0}^{m_{k}} \beta_{i}(k)=1$

为了使PDA与卡尔曼滤波在运算上相匹配, 修改卡尔曼滤波更新阶段的算法, 将残差修改为概率加权残差:

\[\begin{aligned} \hat{\mathbf{x}}_{k \mid k} &=\sum_{i=0}^{m_{k}} \hat{\mathbf{x}}_{i, k \mid k} \beta_{i}(k) \\ &=\hat{\mathbf{x}}_{k \mid k-1} \sum_{i=0}^{m_{k}} \beta_{i}(k)+\mathbf{K}_{k} \sum_{i=0}^{m_{k}}\left(\mathbf{y}_{i, k}-\mathbf{M}_{k} \hat{\mathbf{x}}_{k \mid k-1}\right) \beta_{i}(k) \\ &=\hat{\mathbf{x}}_{k \mid k-1}+\mathbf{K}_{k} \mathbf{\Psi}_{k} \end{aligned}\]

其中，

\[\boldsymbol{\Psi}_{k}=\sum_{i=1}^{m_{k}}\left(\mathbf{y}_{i, k}-\mathbf{M}_{k} \hat{\mathbf{x}}_{k \mid k-1}\right) \beta_{i}(k)\]

可以视为PDA算法下的等效残差。

根据文献 $[12]$, 误差协方差矩阵 $\mathbf{P}_{k \mid k}$ 修改为:

\[\mathbf{P}_{k \mid k}=\beta_{0}(k) \mathbf{P}_{k \mid k-1}+\left[1-\beta_{0}(k)\right] \mathbf{P}_{k \mid k}^{0}+\widetilde{\mathbf{P}}_{k}\]

其中,

\[\quad \mathbf{P}_{k \mid k}^{0}=\left(\mathbf{I}-\mathbf{K}_{k} \mathbf{M}_{k}\right) \mathbf{P}_{k \mid k-1}\] \[\widetilde{\mathbf{P}}_{k}=\mathbf{K}_{k}\left[\sum_{i=1}^{m_{k}} \beta_{i}(k) \widetilde{\mathbf{y}}_{i, k} \tilde{\mathbf{y}}_{i, k}^{\mathbf{T}}-\tilde{\mathbf{y}}_{i, k} \tilde{\mathbf{y}}_{i, k}^{\mathbf{T}}\right] \mathbf{K}_{k}^{\mathbf{T}}\]

补充说明，第 $i$ 个候选拍的测量残差 $\widetilde{\mathbf{y}}_{i,k}=\mathbf{y}_{i,k}-\hat{\mathbf{y}}_{k \mid k-1}$。

在原有卡尔曼滤波算法的基础上，引入多个观测候选值 y 以及对应的权值系数 bta，在Matlab对卡尔曼滤波算法修改如下:

% % % KalmanFilterPDA.m % % %
% Predict
xp = A * x;
Pp = A * P * A' + Q;

% Update
K = Pp * M' / ( M * Pp * M' + R);
x = xp + K * sum((y - M * xp) .* bta);
P0 = ( eye(2) - K * M ) * Pp;
yh = y - M * xp;
Ph = K * ( sum( bta * (yh * yh') ) - yh * yh' )  * K';
P = bta0 * Pp + (1 - bta0) * P0 + Ph;  

统计强度概率分布

根据PDA的要求，我们需要一个先验的候选拍真实与否关于重音强度的概率分布。使用MIREX06数据集，其包含20段长度30s的音频train*.wav，每一段都由40个测试人员分析其节拍，文件train*.txt记录了拍子的位置。

测试人员给出的拍子将作为基本真值（gound truth），对真实拍子的重音强度进行统计，得到如下直方图（蓝色是节拍音的分布，橙色是非节拍音）：

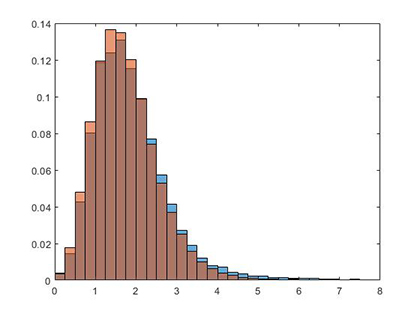
intensity

可见两者无明显差异，且和文献相去甚远：

分析数据集，可见基本真值的分布较为分散，并不准确落在重音拍上。

truth_train1

那么接下来的工作有三个选择：

把基本真值定位到重音上，比如用LM做对真实拍集中的点位做峰值选取；
修改检测函数，比如改变做差分的频段，使其对重音更加敏感；
直接采用文献给出的概率分布。

两个评价指标

P-Score：
\[P=\frac{1}{N_{\max }} \sum_{n=-\infty}^{\infty} \sum_{m=-W}^{W} \delta_{d}(n) \delta_{g}(n-m)\]
$\delta_d$ 和 $\delta_g$ 是检测到的牌子位置和真实拍子位置的单位脉冲序列，但赋值只取0或1；

$ N_{\max }=\max \left(N_{d}, N_{g}\right) $ 是检测到的拍子数量$N_d$和真实拍子数量$N_g$中的最大值；

$2W$ 是采样窗口宽度，实验取拍子持续时间的20%.
LTMSR：

最长跟踪时间比率(LTMSR): 即正确跟踪的最长时长与总时长的比值，侧重于持续跟踪性能。