对于许多应用来说,数据集里的数据点独立同分布的假设不成立。顺序数据的数据集通常产⽣于沿着时间序列进⾏的测量,例如某个特定位置的连续若⼲天的降⽔量测量,或者每天汇率的值,或者对于语⾳识别任务,在连续的时间框架下的声学特征。
考虑未来的观测对所有之前的观测的⼀个⼀般的依赖关系是不现实的, 因为这样⼀个模型的复杂度会随着观测数量的增加⽽⽆限制地增长。马尔科夫模型(Markov model)假定未来的预测仅与最近的观测有关,⽽独⽴于其他所有的观测。
通过引⼊潜在变量,可以得到⼀个更加⼀般的框架,同时仍然保持计算上的可处理性,这就引出了状态空间模型(state space model)。
- 潜在变量是离散:隐马尔可夫模型(hidden Markov model)。
- 潜在变量服从⾼斯分布:线性动态系统(linear dynamical system)。
区分两个重要概念:
- 静⽌分布:数据会随着时间发⽣变化,但是⽣成数据的概率分布保持不变。
- ⾮静⽌分布:⽣成概率本⾝会随着时间变化。
我们关注的是静⽌分布的情形。
马尔科夫模型

图13.2 对顺序观测建模的最简单的方法是将它们看做独立的,对应于没有链接的图。
假设右侧的每个条件概率分布只与最近的一次观测有关,而独立于其他所有之前的观测,那么我们就得到了一阶马尔科夫链(first-order Markov chain)

图13.3 观测 $\{x_n\}$ 的⼀阶马尔科夫链,其中特定的观测$ x_n $依赖于前一次观测$ x_{n−1} $的值。
这个模型中,$ N $次观测的序列的联合概率分布为
\[p(x_1,...,x_N) = p(x_1)\prod\limits_{n=2}^Np(x_n\mid x_{n-1})\]给定时刻$ n $之前的所有观测,我们看到观测$ x_n $的条件概率分布为
\[p(x_n\mid x_1,...,x_{n-1}) = p(x_n\mid x_{n-1})\]条件概率分布$ p(x_n\mid x_{n−1}) $被限制为相等的,对应于静止时间序列的假设。这样,这个模型被称为同质马尔科夫链(homogeneous Markov chain)。
如果我们允许预测除了与当前观测有关以外,还与当前观测的前一次观测有关,那么我们就得到了二阶马尔科夫链
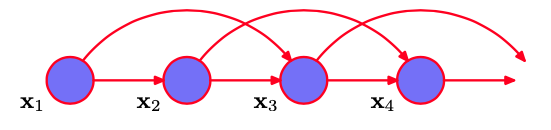
图13.4 观测 $\{x_n\}$ 的二阶马尔科夫链,其中特定的观测$ x_n $依赖于前两次观测$ x_{n−1} $和$ x_{n−2} $的值。
联合概率分布
\[p(x_1,...,x_N) = p(x_1)p(x_2\mid x_1)\prod\limits_{n=3}^Np(x_n\mid x_{n-1},x_{n_2})\]现在假设我们将模型推广到$ M $阶马尔科夫链,从而联合概率分布由条件概率分布$ p(x_n\mid x_{n−M},…,x_{n-1}) $构建。如果变量是离散变量,且条件概率分布使用一般的条件概率表的形式表示,那么这种模型中参数的数量为$ K^M (K − 1) $。 由于这个量随着$ M $指数增长,因此通常对于大的$ M $来说,使用这种方法是不实际的。
对于连续变量来说,我们可以使用线性高斯条件概率分布,其中每个结点都是一个高斯概率分布,均值是父结点的一个线性函数。这被称为自回归(autoregressive)模型或者AR模型。
另一种方法是为$ p(x_n\mid x_{n−M},…, x_{n-1}) $使用参数化的模型,例如神经网络。这种方法有时被称为抽头延迟线(tapped delay line),因为它对应于存储(延迟)观测变量的前面$ M $个值来预测下一个值。这样,参数的数量远远小于一个一般的模型(例如此时参数的数量可能随着$ M $线性增长),虽然这样做会使得条件概率分布被限制在一个特定的类别中。
假设我们希望构造任意阶数的不受马尔科夫假设限制的序列模型,同时能够使用较少数量的自由参数确定。我们可以引入额外的潜在变量来使得更丰富的一类模型能够从简单的成分中构建。对于每个观测$ x_n $,我们引入一个对应的潜在变量$ z_n $(类型或维度可能与观测变量不同)。我们现在假设潜在变量构成了马尔科夫链,得到的图结构被称为状态空间模型(state space model)。
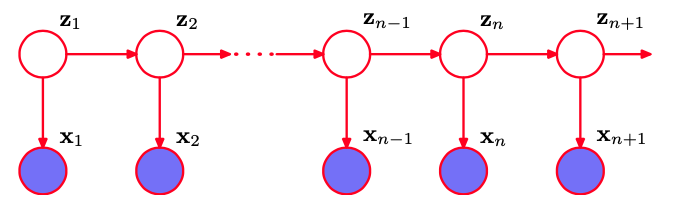
图13.5 可以使用潜在变量的马尔科夫链来表示顺序数据,每个观测都以对应的潜在变量的状态为条件。这个重要的图结构组成了隐马尔科夫模型和线性动态系统的基础。
它满足下面的关键的条件独立性质,即给定$ z_n $的条件下,$ z_{n−1} $和$ z_{n+1} $是独立的,从而
\[z_{n+1} \perp z_{n-1}\mid z_n\]这个模型的联合概率分布为
\[p(x_1,...,x_N,z_1,...,z_N) = p(z_1)\left[\prod\limits_{n=2}^Np(z_n\mid z_{n-1})\right]\prod\limits_{n=1}^Np(x_n\mid z_n)\]使用d-划分准则,我们看到总存在一个路径通过潜在变量连接了任意两个观测变量$ x_n $和$ x_m $,且这个路径永远不会被阻隔。因此对于观测变量$ x_{n+1} $来说,给定所有之前的观测,条件概率分布$ p(x_{n+1} \mid x_1,…,x_n) $不会表现出任何的条件独立性,因此我们对$ x_{n+1} $的预测依赖于所有之前的观测。
如果潜在变量是离散的,那么我们得到了隐马尔科夫模型(hidden Markov model)。注意,HMM中的观测变量可以是离散的或者是连续的,并且可以使用许多不同的条件概率分布进行建模。
如果潜在变量和观测变量都是高斯变量(结点的条件概率分布对于父结点的依赖是线性高斯的形式),那么我们就得到了线性动态系统(linear dynamical system)。
隐马尔可夫模型
如果我们考察模型的一个单一的时间切片,那么我们看到它对应于一个混合概率分布,对应的分量密度为$ p(x\mid z) $。于是,它也可以表述为混合概率模型的一个推广,其中每个观测的混合系数不是独立地选择的,而是依赖于对于前一次观测的分量的选择。潜在变量是离散的服从多项式分布的变量$ z_n $,描述了那个混合分量用于生成对应的观测$ x_n $。比较方便的做法是使用1-of-K表示方法。
我们现在让$ z_n $的概率分布通过条件概率分布$ p(z_n \mid z_{n−1}) $对前一个潜在变量$ z_{n−1} $产生依赖。由于潜在变量是K维二值变量,因此条件概率分布对应于数字组成的表格,记作$ A $,它的元素被称为转移概率(transition probabilities)。
元素为$ A_{jk} \equiv p(z_{nk} = 1\mid z_{n−1}, j = 1) $。由 于它们是概率值,因此满足$ 0 \leq A_{jk} \leq 1 $且$ \sum_k A_{jk} = 1 $,从而矩阵$ A $有$ K(K − 1) $个独立的参数。这样,我们可以显式地将条件概率分布写成
\[p(z_n\mid z_{n-1},A) = \prod\limits_{k=1}^K\prod\limits_{j=1}^KA_{jk}^{z_{n-1, j}z_{nk}}\]初始潜在结点$ z_1 $很特别,因为它没有父结点,因此它的边缘概率分布$ p(z_1) $由一个概率向量$ \pi $表示,元素为$ \pi_k \equiv p(z_{1k} = 1) $,即
\[p(z_1 \mid \pi) = \prod\limits_{k=1}^K\pi_k^{z_{1k}}\]其中$ \sum_k\pi_k = 1 $。
有时可以将状态画成状态转移图中的一个结点,这样就可以图形化地表示出转移矩阵。图13.6给出了K = 3的情形。
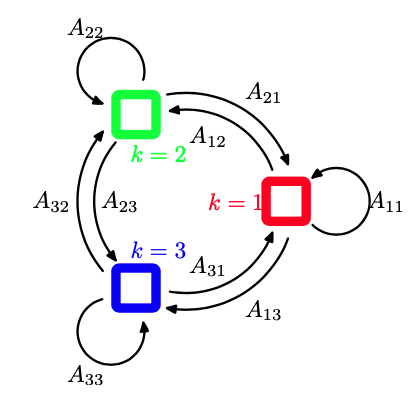
图13.6 转移图表示一个模型,它的潜在变量有三种可能的状态,对应于三个方框。黑线表示转移矩阵的元素$ A_{jk} $。
注意,这不是一个概率图模型,因为结点不是单独的变量而是一个变量的各个状态,因此我们用方框而不是圆圈来表示状态。
有时比较有用的做法是将图13.6所示的状态转移图在时间上展开。这给出了潜在变量之间转移的另一种表示方法,被称为晶格图(lattice diagram)或格子图(trellis diagram)。
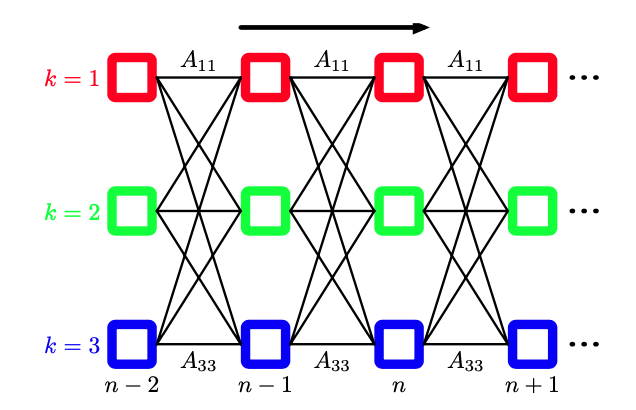
图13.7 状态转移图在时间上展开,那么我们旧得到了潜在状态的晶格图表示或格子图表示。图的每一列对应于一个潜在变量$ z_n $。
可以通过定义观测变量的条件概率分布$ p(x_n\mid z_n,\phi) $来确定一个概率模型,其中$ \phi $是控制概率分布的参数集合。这些条件概率被称为 发射概率 (emission probabilities),可以是例如
\[p(x\mid z) = \prod\limits_{k=1}^K\mathcal{N}(x\mid \mu_k,\Sigma_k)^{z_k}\]这样的高斯分布($ x $是连续变量),也可以是条件概率表格($ x $是离散变量)。由于$ x_n $是观测值,因此对于一个给定的$ \phi $值,概率分布$ p(x_n\mid z_n,\phi) $由一个$ K $维的向量组成,对应于二值向量$ z_n $的$ K $个可能的状态。我们可以将发射概率表示为
\[p(x_n\mid z_n,\phi) = \prod\limits_{k=1}^Kp(x_n\mid \phi_k)^{z_{nk}}\]我们将注意力集中在同质的(homogeneous)模型上,其中所有控制潜在变量的条件概率分布都共享相同的参数$ A $,类似地所有发射概率分布都共享相同的参数$ \phi $(推广到更一般的情形很容易)。注意,对于一个独立同分布的数据集,一个混合模型对应于参数$ A_{jk} $对于所有的$ j $值都相同的情况,从而条件概率分布$ p(z_n\mid z_{n−1}) $与$ z_{n−1} $无关。
从而观测变量和潜在变量上的联合概率分布为
\[p(X,Z\mid \theta) = p(z_1\mid \pi)\left[\prod\limits_{n=2}^N p(z_n\mid z_{n−1},A)\right]\prod\limits_{m=1}^Np(x_m\mid z_m,\phi)\]其中$ X = {x_1,…,x_N}, Z = {z_1,…,z_N} $ 和 $ \theta = {\pi,A,\phi} $表示控制模型参数的集合。我们关于隐马尔科夫模型的大部分讨论与发射概率的特定选择无关。事实上,模型对于一大类发射概率的选择都是可以计算的,包括离散表格、高斯以及混合高斯。也可以利用判别式模型例如神经网络。这些可以用来直接对发射概率密度$ p(x\mid z) $建模,也可以用来给出$ p(z\mid x) $的一个表达式,这个表达式可以使用贝叶斯定理转化为所需的发射概率密度$ p(x\mid z) $。
从生成式的观点考虑隐马尔科夫模型,我们可以更好地理解隐马尔科夫模型。回忆一下,为了从一个混合高斯分布中生成样本,我们首先随机算一个分量,选择的概率为混合系数$ \pi_k $,然后从对应的高斯分量中生成一个样本向量$ x $。这个过程重复$ N $次,产生$ N $个独立样本组成的数据集。 在隐马尔科夫模型的情形,这个步骤修改如下。首先我们选择初始的潜在变量$ z_1 $,概率由参数$ \pi_k $控制,然后采样对应的观测$ x_1 $。现在我们使用已经初始化的$ z_1 $的值,根据转移概率$ p(z_2\mid z_1) $来选择变量$ z_2 $的状态。从而我们以概率$ A_{jk} $选择$ z_2 $的状态$ k $,其中$ k = 1,…,K $。一旦我们知道了$ z_2 $,我们就可以对$ x_2 $采样,从而也可以对下一个潜在变量$ z_3 $采样,以此类推。这是有向图模型的祖先采样的一个例子。例如,如果我们有一个模型,其中对角转移元素$ A_{kk} $比非对角的元素大得多,那么一个典型的数据序列中,会有连续很长的一系列点由同一个概率分布生成,而从一个分量转移到另一个分量不会经常发生。
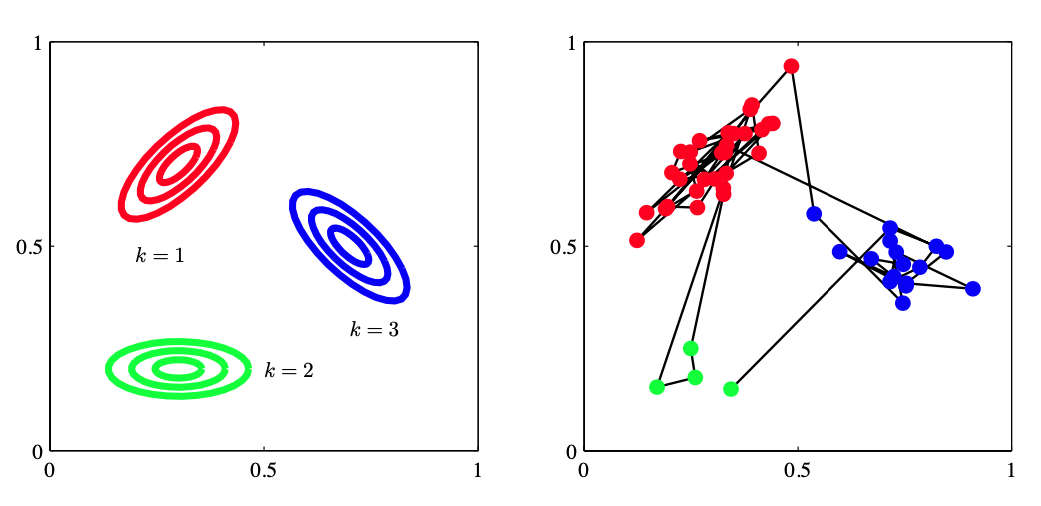
图13.8 从一个隐马尔科夫模型中进行采样的例子,这个模型的潜在变量z有三个状态,发射概率$ p(x\mid z) $是高斯概率,其中$ x $是二维的。(a)发射概率密度为常数的轮廓线,对应于潜在变量的三个状态。(b)从隐马尔科夫模型中抽取的50个样本点,数据点的颜色对应于生成它们的分量的颜色,数据点之间的连线表示连续的观测。这里,转移矩阵是固定的。在任何状态,都有5%的概率转移到每个其他的状态,有90%的概率保持相同的状态。
线性动态系统
HMM的一个重要的特性是它的潜在变量是离散的,但发射概率分布是任意的。将潜在变量推广为连续的,保留推断的高效算法,在每个阶段概率分布都不可以变复杂,而仅仅在参数上发生变化,就得到线性动态系统(LDS)。例如,在给定观测 $x_1,\dots,x_n$ 的条件下,表示 $z_{n-1}$ 的后验分布的量 $\hat{\alpha}(z_{n-1})$ 在与转移概率 $p(z_n\mid z_{n-1})$ 和发射概率 $p(x_n\mid z_n)$ 相乘然后在 $z_{n-1}$ 上求和或积分后得到的 $z_n$ 上的概率分布与 $\hat{\alpha}(z_{n-1})$ 上的概率分布具有相同的形式。而在多次相乘之后仍然具有不变形式的唯一分布就是指数族分布的成员,实际应用上最重要的例子是高斯分布。
- 前向递归方程,称为 Kalman 滤波,类似于 HMM 的 $\alpha$ 信息
- 后向递归方程,称为 Kalman 平滑,类似于 HMM 的 $\beta$ 信息
由于模型的条件概率分布是高斯分布,我们可以将转移分布和发射分布写成如下的形式
\[p(z_n \mid z_{n-1})=\mathcal{N}(z_n\mid A z_{n-1},\Gamma) \\ p(x_n \mid z_n)=\mathcal{N}(x_n\mid C z_n,\Sigma)\]其中 $A$ 是转移矩阵,$\Gamma$ 是转移噪声的协方差矩阵,$C$ 是发射矩阵,$\Sigma$ 是发射噪声的协方差矩阵。初始潜在变量 $z_1$ 的分布为 \(p(z_1) = \mathcal{N}(z_1\mid \mu_0,P_0)\),其中 $\mu_0$ 是均值,$P_0$ 是协方差矩阵。
传统上,这些概率分布通常使用噪声线性方程表示为一个等价的形式
\[z_n = A z_{n-1} + w_n \\ x_n = C z_n + v_n \\ z_1 = \mu_0 + u_0\]其中噪声项的概率分布为
\[w\sim \mathcal{N}(w\mid 0,\Gamma)\\ v \sim \mathcal{N}(v\mid 0,\Sigma)\\ u \sim \mathcal{N}(u\mid 0,P_0)\]模型的参数被记为 \(\theta = \left\{ A,\Gamma,C,\Sigma,\mu_0,P_0 \right\}\),可以通过EM算法使用最大似然方法进行估计。在E步骤中,需要计算后验概率 $p(z_n\mid x_1,\dots,x_N)$,可以使用加和-乘积算法高效求出。
LDS中的推断
考虑前向方程,将 $z_N$ 看做根节点,然后从叶节点 $h(z_1)$ 将信息传递到根结点,传递的信息是归一化的边缘概率分布,对应于 $p(z_n\mid x_1,\dots,x_n)$,将其记为 $\hat{\alpha}(z_n) = \mathcal{N}(z_n \mid \mu_n, V_n)$。因此,递归方程为
\[c_n \hat{\alpha}(z_n) = p(x_n\mid z_n) \int \hat{\alpha}(z_{n-1}) p(z_n\mid z_{n-1}) \mathrm{d} z_{n-1}\]