拉格朗日对偶问题

当优化问题是非凸优化问题时候，如果我们的问题满足一定的条件，那么可以通过求解对偶问题将原问题转化为凸优化问题。

原问题的等价

我们先来看一个最简单的例子，我们的原问题是

\[\begin{aligned} \min \quad & f_0(x), \quad x \in \mathbb{R}^n\\ \text{s.t.} \quad & f_i(x) \leq 0, \quad i = 1, \cdots, m \\ & h_i(x) = 0, \quad i = 1, \cdots, q \end{aligned} \tag{1}\]

其中 $f_i(x)$ 是不等式约束，$h_i(x)$ 是等式约束，交集称为可行域。

我们可以将其写成拉格朗日函数的形式：

\[L(x, \lambda, \nu) = f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \tag{2}\]

其中，$\lambda_i$和$\nu_i$是拉格朗日乘子。于是，可以将原问题写成对拉格朗日函数求两次最值的形式：

\[\begin{aligned} \min_{x}\ \max_{\lambda, \nu} & \ L(x, \lambda, \nu) \\ \text{s.t.} \quad & \lambda_i \geq 0, \quad i = 1, \cdots, m \end{aligned} \tag{3}\]

注意到 $x$ 的取值范围已经变成全空间 $\mathbb{R}^n$。我们可以通过下面的推导来证明$(1)\Leftrightarrow(3)$：

$1$. 当$x$不在原可行域内，即$f_i(x) > 0$ 或者 $h_i(x)\ne 0$，由于 $\lambda, \nu$的取值可以是 $\infty$，所以总有

\[\max_{\lambda, \nu} \left( \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \right) = \infty\]

$2$. 当$x$在原可行域内，即$f_i(x)\le 0, h_i(x)=0, \lambda_i \ge 0$，于是有

\[\max_{\lambda, \nu} \left( \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \right) = 0 + 0 =0\]

所以，我们可以得到

\[\min_{x} \ \max_{\lambda, \nu} \ L(x, \lambda, \nu) = \min_{x}\left(f_0(x), \infty \right) = \min_{x} f_0(x)\]

证毕。

接下来给出拉格朗日对偶问题的定义。

定义对偶函数

\[g(\lambda,\nu) = \min_{x} \ L(x, \lambda, \nu) \tag{4}\]

$(3)$的拉格朗日对偶问题为

\[\begin{aligned} \max_{\lambda, \nu} \ & g(\lambda,\nu) = \max_{\lambda, \nu} \ \min_{x} \ L(x, \lambda, \nu) \\ \text{s.t.} \quad & \lambda_i \geq 0, \quad i = 1, \cdots, m \end{aligned} \tag{5}\]

相当于交换了$(3)$中的$\min$和$\max$运算。

那么，对偶问题和原问题的关系是什么呢？答案是：对偶问题的目标函数是原问题的下界。证明如下：

对于任意的$\lambda, \nu$，下式恒成立

\[\max_{\lambda, \nu} \ L(x, \lambda, \nu) \ge L(x, \lambda, \nu) \ge \min_{x} \ L(x, \lambda, \nu)\]

对左边取最小值，对右边取最大值，上式依然成立

\[\min_{x} \ \max_{\lambda, \nu} \ L(x, \lambda, \nu) \ge \max_{\lambda, \nu} \ \min_{x} \ L(x, \lambda, \nu)\]

证毕。

对偶问题是凸问题

这里不加证明的给出几个引理：

$\quad 1$. 如果对于任意 $ x_1, x_2 \in C$，有 $\theta \in [0,1]$，使得 $\theta x_1 + (1-\theta) x_2 \in C$，则称 $C$ 是凸集。

$\quad 2$. 对于 $x\in\mathbb{R}^n, W \in \mathbb{R}^n, b\in \mathbb{R}$，集合$H=\left\{x \mid W^{\top}x+b\le 0\right\}$是半空间。

$\quad 3$. 对于 $x\in\mathbb{R}^n, W \in \mathbb{R}^n, b\in \mathbb{R}$，集合$A = \left\{x \mid W^{\top}x+b= 0\right\}$是仿射集。

$\quad 4$. 半空间 $H$，仿射集 $A$ 及其交集是凸集。

$\quad 5$. 当目标函数必须是凸函数，约束条件的可行域是凸集时，问题为凸优化问题。

设 $x^* = \underset{x}{\arg\min}\ L(x,\lambda,\nu) $，则对偶函数$(4)$可写为

\[g(\lambda,\nu) = f_0(x^*) + \sum_{i=1}^m \lambda_i f_i(x^*) + \sum_{i=1}^q \nu_i h_i(x^*)\]

其中，$f_0(x^*), f_i(x^*), h_i(x^*)$ 都是常数，所以 $g(\lambda,\nu)$ 是关于 $\lambda$ 和 $\nu$ 的仿射函数，可行域$\lambda_i \ge 0$ 为半空间，所以对偶问题$(5)$是凸问题。

对偶问题与原问题的关系

现在我们知道，对偶问题的目标函数是原问题的下界，对偶问题是凸问题，而凸问题的求解是方便的。什么时候对偶问题的解也等于原问题的解呢？答案是：绝大多情况下，原问题满足KKT条件即可。但严格的数学表述下：KKT条件只是必要条件，Slater条件是充分条件，但充要条件现在还没找到。

在约束条件$h_i(x)=0$下，令 $t=f_0(x), u_i = f_i(x)$。让我们重新表述一下拉格朗日函数$(2)$：

\[L(t,u) = t + \lambda^{\top}u \tag{6}\]

那么，原问题$(1)$可以写成

\[\min_x \ \{ t \mid (t,u) \in G_1\} \\ \text{s.t.} \quad G_1 = \left\{ (t,u)\mid t=f_0(x), u_i = f_i(x) \le 0,x\in D \right\} \tag{7}\]

其中$D$是原问题$(1)$的可行域。

对偶问题$(5)$可以写成

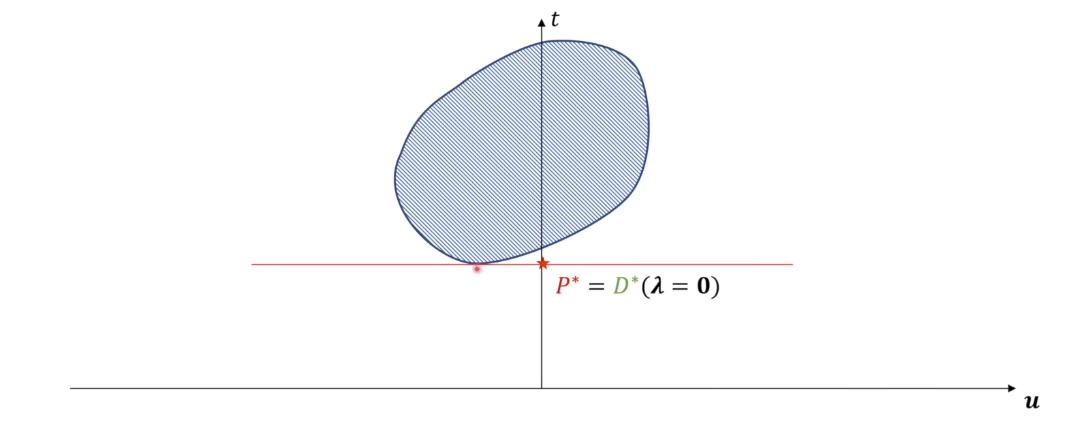
\[\max_{\lambda, \nu}\ \min_x \ \{ t + \lambda^\top u \mid (t,u) \in G_2, \lambda\ge 0\} \\ \text{s.t.} \quad G_2 = \left\{ (t,u)\mid t=f_0(x), u_i = f_i(x), x\in \mathbb{R}^n \right\} \tag{8}\]

假设$G_2$的形状如下图所示（弧形包裹区域），由于$G_1$ 为$G_2$中满足 $ u_i = f_i(x) \le 0 $的部分，因此 $G_1$ 只占据$G_2$ 中 $u$ 负半轴深色网格区域。可见，转化后的原问题$(7)$的最优取值为 $P^*$：

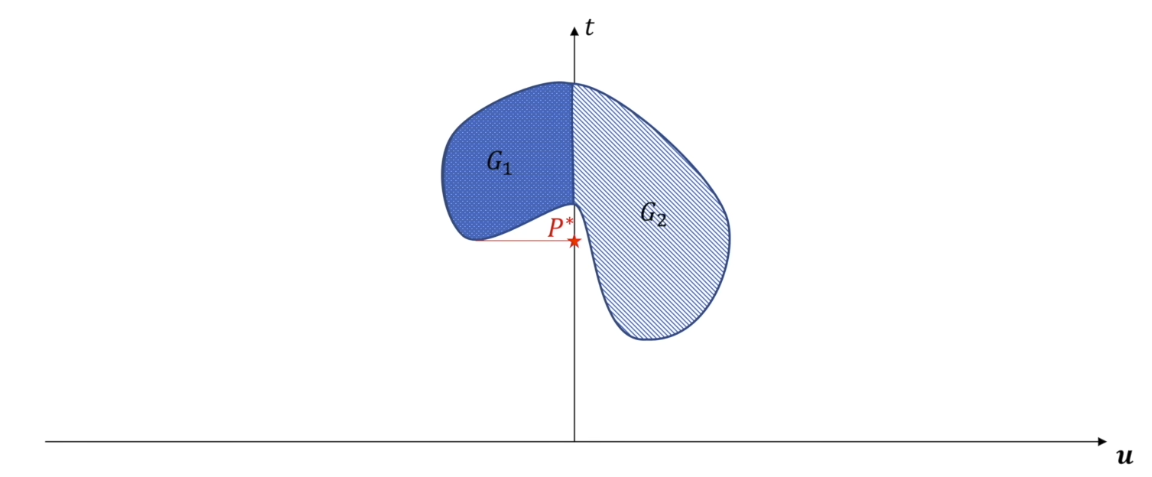
Alt text

对于转化后的对偶问题$(8)$，注意到只有约束$\lambda \ge 0$和$(t,u) \in G_2$。于是，首先固定 $\lambda$ 求解$\underset{x}{\min}\ t + \lambda^\top u$，即固定了一条直线$t+\lambda^\top u $中的斜率，移动截距找到最小值$D^*$。

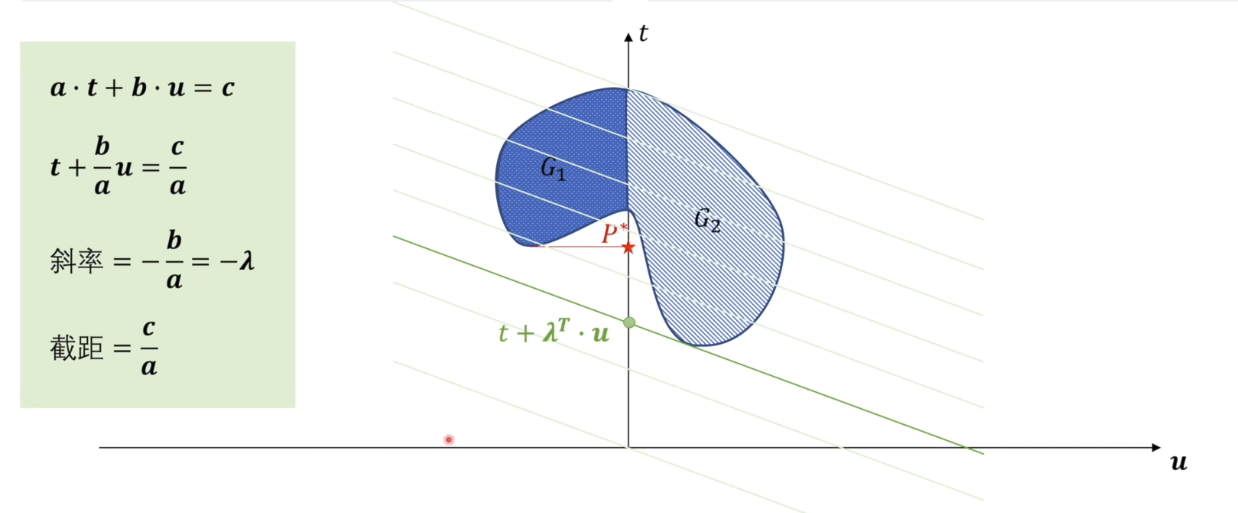
Alt text

然后就可以移动斜率$-\lambda$，找到最大值$D^*$，即对偶问题的最优取值，就是直线和 $G_1，G_2$ 同时相切的情况。因为如果直线穿过了$G_1$，则不能满足上一步$\underset{x}{\min}\ t + \lambda^\top u$。

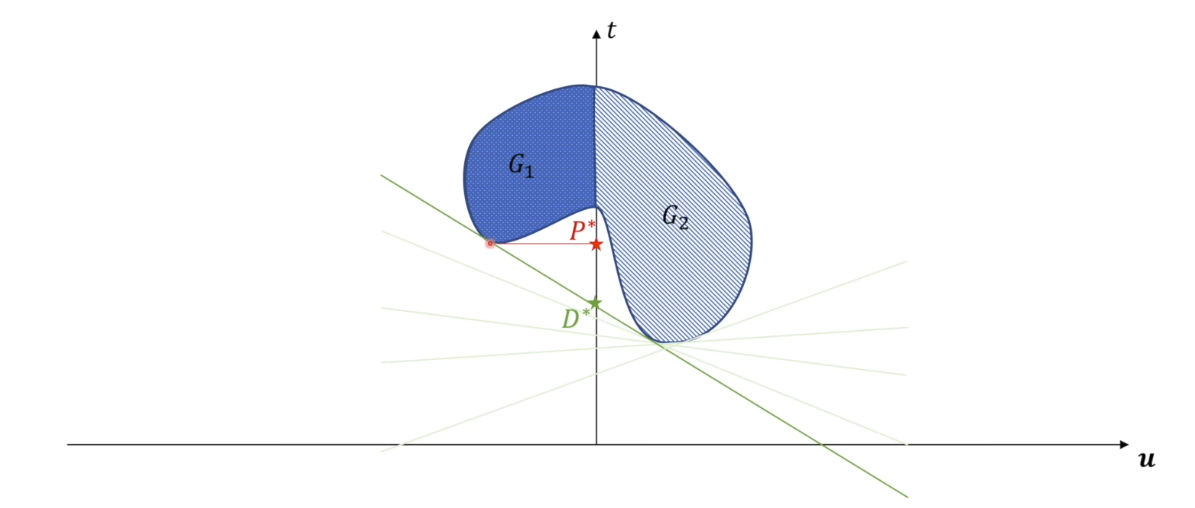
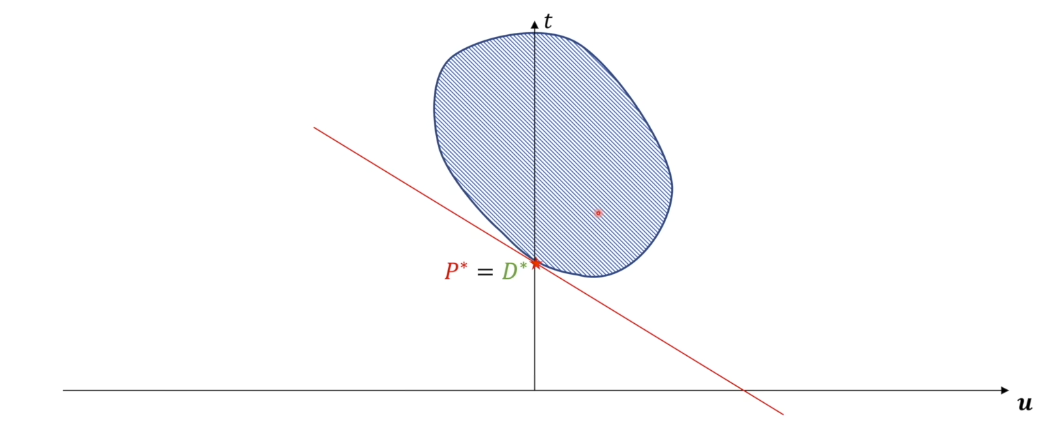
Alt text

这是$G_2$是非凸集，而且最优$u$在右半边的情况。而当$G_2$是凸集，或者最优$u$在左半边时，总有 $P^* \ge D^*$，这时我们把原问题和对偶问题叫做一种 弱对偶关系。而当$G_2$是凸集，或者最优$u$在左半边时，总有 $P^* = D^*$ ，这时我们把原问题和对偶问题叫做一种强对偶关系，即对偶问题的最优解等于原问题的最优解。

Alt text