PRML笔记 Ch1.绪论

1.1. 示例：多项式曲线拟合

多项式拟合函数

\[y(x,w)=w_0+w_1x+w_2x^2+...+w_Mx^M=\sum_{j=0}^M {w_jx^j} \tag{1.1}\]

一个简单的应用广泛的误差函数是每个数据点xn的预测值y(xn,w)与目标值tn的平方和

\[E(w) = \frac{1}{2} \sum^{N}_{n=1}\{y(x_n,w)- tn\}^2 \tag{1.2}\]

目标是让误差函数越来越小。有唯一解 $w^*$ ,是的 $E(w)$ 取得最小值 $E(w^*)$ 。

m太大发生过拟合，泛化性能下降。需要一个衡量模型泛化能力的标准。

解决方法：1.增加样本数量。 2.正则化。

为了比较不同大小的数据集和保证和t有相同单位。引入均方根误差：

\[E_{R M S}=\sqrt{2 E\left(\boldsymbol{w}^{*}\right) / N} \tag{1.3}\]

正则化

给误差函数 （1.2）增加⼀个惩罚项，使得系数不会达到很⼤的值。这种惩罚项最简单的形式采⽤所有系数的平⽅和的形式。

\[\tilde{E}(\boldsymbol{w})=\frac{1}{2} \sum_{n=1}^{N}\left\{y\left(x_{n}, \boldsymbol{w}\right)-t_{n}\right\}^{2}+\frac{\lambda}{2}\mid \boldsymbol{w}\mid ^{2} \tag{1.4}\]

$\mid w\mid ^2 =w^T w=w^2_0 + w^2_1 + … + w^2_M$ 系数$\lambda$控制了正则化项相对于平方和误差项的重要性。

注意，通常系数$w_0$从正则化项中省略，因为包含$w_0$会使得结果依赖于目标变量原点的选择.

寻找模型参数最⼩平⽅⽅法代表了最⼤似然（maximum likelihood）（将在1.2.5节讨论）的⼀种特殊情形，并且过拟合问题可以被理解为最⼤似然的⼀个通⽤属性。通过使⽤⼀种贝叶斯（Bayesian）⽅法，过拟合问题可以被避免。

1.2 概率论

加法法则

\[p(X)=\sum_{Y}p(X,Y) \tag{1.10}\]

乘积法则

\[p(X,Y)=P(Y\mid X)p(X) \tag{1.11}\]

根据这两个式子得到本书最重要的定义：贝叶斯定理。

\[P(Y \mid X)=\frac{P(X \mid Y) P(Y)}{P(X)} \tag{1.12}\]

分子中的$P(x)=\sum_{Y}P\left(X \mid Y\right)P\left(Y\right)$其实这就是加法规则。确保了概率在归一化之后的值为1。

1.2.1 概率密度

如果一个实值变量$x$落在区间$(x, x + \delta x)$的概率由$p(x)\delta x$给出，其中$ \delta x \to 0 $，那么我们就把$ p(x) $称作$ x $的概率密度（probability density）。 连续概率分布：

\[p(x \in(a, b))=\int_{a}^{b} p(x) \mathrm{d}x \tag{1.24}\]

满足：

\[p(x)\geq0 \tag{1.25}\] \[\int_{-\infty}^{\infty} p(x) \mathrm{d}x=1 \tag{1.26}\]

可以用过Jacobian因子变化：例如:$x=g(y)$

\[p_{y}(y)=p_{x}(x)\left| \frac{\mathrm{d} x}{\mathrm{d} y}\right| =p_{x}(g(y))\left| g^{\prime}(y)\right| \tag{1.27}\]

概率密度最大值的概念取决于变量的选择。

累计密度分布：

\[P(z) = \int_{-\infty}^z p(x)dx \tag{1.28}\]

满足$ P^\prime(x) = p(x) $

加法法则和乘法法则

\[p(x) = \int p(x, y) dy \tag{1.31}\] \[p(x, y)= p(y\mid x)p(x) \tag{1.32}\]

1.2.2 期望和方差

概率的加和规则和乘积规则以及贝叶斯规则，同样可以应⽤于概率密度函数的情形。

例如，如果x和y 是两个实数变量，那么在概率分布p(x)下，函数f(x)的平均值被称为f(x)的期望（expectation），记作$E[f]$。对于离散变量，它的定义为

\[\mathbb{E}[f]=\sum_{x} p(x) f(x)(离散) \tag{1.33}\] \[\mathbb{E}[f]= \int p(x){f}(x) \mathrm{d}x(连续) \tag{1.34}\]

考虑多变量函数的期望，可以使⽤下标来表明被平均的是哪个变量，例如$\mathbb{E}_x[f(x,y)]$是y 的⼀个函数。

条件分布的期望：条件期望（conditional expectation）

\[\mathbb{E}_{x}[f \mid y]=\sum_{x} p(x \mid y) f(x) \tag{1.37}\]

f(x)的⽅差（variance）

\[\mathrm{var}(f) = \mathbb{E}[(f(x)-\mathbb{E}[f(x)])^2] \tag{1.38}\]

考虑变量x⾃⾝的⽅差，它由下式给出：

\[\mathrm{var}(x) = \mathbb{E}[x^2]-\mathbb{E}[x]^2 \tag{1.39}\]

对于随机变量x,y，协方差定义为

\[\mathrm{cov}(x,y) = \mathbb{E}_{xy}[\{x-\mathbb{E}[x]\}\{y-\mathbb{E}[y]\}] \tag{1.41}\\ =\mathbb{E}_{xy}[xy]-\mathbb{E}[x]\mathbb{E}[y]\]

证明：

\[\begin{split} \mathrm{cov}(x,y)&=\mathbb{E}_{xy}[xy-x\mathbb{E}[y]-y\mathbb{E}[x]+\mathbb{E}[x]\mathbb{E}[y]]\\ &=\mathbb{E}_{xy}[xy]-\mathbb{E}[x]\mathbb{E}[y]-\mathbb{E}[x]\mathbb{E}[y]+\mathbb{E}[x]\mathbb{E}[y]\\ &=\mathbb{E}_{xy}[xy]-\mathbb{E}[x]\mathbb{E}[y] \end{split}\]

如果x和y是独立的，则它们的协方差消失。

在随机变量x和y的两个向量的情况下，协方差是一个矩阵

\[\begin{aligned} \operatorname{cov}[\mathbf{x}, \mathbf{y}] &=\mathbb{E}_{\mathbf{x}, \mathbf{y}}\left[\{\mathbf{x}-\mathbb{E}[\mathbf{x}]\}\left\{\mathbf{y}^{\mathrm{T}}-\mathbb{E}\left[\mathbf{y}^{\mathrm{T}}\right]\right\}\right] \\ &=\mathbb{E}_{\mathbf{x}, \mathbf{y}}\left[\mathbf{x} \mathbf{y}^{\mathrm{T}}\right]-\mathbb{E}[\mathbf{x}] \mathbb{E}\left[\mathbf{y}^{\mathrm{T}}\right] \end{aligned}\tag{1.42}\]

1.2.3 贝叶斯概率

在观察到数据之前，我们有 ⼀些关于参数 w 的假设，这以先验概率p(w)的形式给出。观测数据$D = { t_1 , \dots, t_N }$ 的效果可以 通过条件概率$ p(D \mid w)$ 表达，我们将在1.2.5节看到这个如何被显式地表达出来。贝叶斯定理的形 式为

\[p(\mathbf{w} \mid \mathcal{D})=\frac{p(\mathcal{D} \mid \mathbf{w}) p(\mathbf{w})}{p(\mathcal{D})} \tag{1.43}\]

它让我们能够通过后验概率 $p(w\mid D)$，在观测到$D$之后估计$w$的不确定性。

贝叶斯定理右侧的量 $p(D \mid w)$ 由观测数据集$D$来估计，可以被看成参数向量 $w$ 的函数，被称为似然函数(likelihood function)。它表达了在不同的参数向量 w 下，观测数据出现的可能性的⼤⼩。注意，似然函数不是 w 的概率分布，并且它关于 w 的积分并不（⼀定）等于1。⽤⾃然语⾔表述贝叶斯定理:

\[posterior∝likelihood × prior \tag{1.44}\]

分母是归一化因子：

\[p(D) = \int p(D\mid w)p(w)dw \tag{1.45}\]

其中所有的量都可以看成 $w$ 的函数。公式（1.43）的分母是⼀个归⼀化常数，确保了左侧的后验概率分布是⼀个合理的概率密度，积分为1。实际上，对公式（1.43）的两侧关于 $w$ 进⾏积分， 我们可以⽤后验概率分布和似然函数来表达贝叶斯定理的分母。

频率学家观点: $w$ 被认为是⼀个固定的参数，频率学家⼴泛使⽤的⼀个估计是最⼤似然（maximum likelihood）估计，其中 $w$ 的值是使似然函数 $p(D \mid w)$ 达到最⼤值的 $w$ 值，这个估计的误差通过考察可能的数据集 $D$ 的概率分布来得到。⼀种决定频率学家的误差的⽅法是⾃助法（bootstrap）。

贝叶斯观点: 只有⼀个数据集 $D$（即实际观测到的数据集），参数w是不固定的，不确定性通过 $w$ 的概率分布来表达。

在机器学习的⽂献中，似然函数的负对数被叫做误差函数（error function）。由于负对数是单调递减的函数，最⼤化似然函数等价于最⼩化误差函数。

1.2.4 ⾼斯分布

⾼斯分布被定义为

\[\mathcal{N}\left(x \mid \mu, \sigma^{2}\right)=\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\} \tag{1.46}\]

⽅差的倒数， 记作 $\beta = \displaystyle\frac{1}{\sigma^2}$ ， 被叫做精度 （precision）.分布的最⼤值被叫做众数。对于⾼斯分布，众数与均值恰好相等。

我们也对D维向量 x 的⾼斯分布也感兴趣，定义为

\[\mathcal{N}(\mathbf{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{(2 \pi)^{D / 2}} \frac{1}{\mid \boldsymbol{\Sigma}\mid ^{1 / 2}} \exp \left\{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^{\mathrm{T}} \boldsymbol{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right\} \tag{1.52}\]

其中D维向量 $\mu$ 被称为均值，D × D的矩阵Σ被称为协⽅差， \mid Σ \mid 表⽰Σ的⾏列式。

现在假定我们有⼀个观测的数据集$x = (x_1, \dots , x_N)^T$，我们假定各次观测是独⽴地从⾼斯分布中抽取的，分布的均值 $\mu$ 和⽅差 $\sigma^2$ 未知，我们想根据数据集来确定这些参数。独⽴地从相同的分布中抽取的数据点被称为独⽴同分布（independent and identically distributed），通常缩写成i.i.d.。

给定 $\mu$ 和 $\sigma^2$ ，我们可以给出数据集的概率

\[p(x\mid\mu,\sigma) = \prod_{n=1}^{N}\mathcal{N}(x_n\mid,\mu,\sigma^2) \tag{1.53}\]

当我们把它看成 $\mu$ 和 $\sigma^2$的函数的时候，这就是⾼斯分布的似然函数。根据公式（1.46）和 公式（1.53），对数似然函数可以写成

\[\begin{split} \ln p(x\mid\mu,\sigma^2) &= \sum_{n=1}^{N}\ln\left\{\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \exp \left(-\frac{1}{2 \sigma^{2}}(x_n-\mu)^{2}\right)\right\} \\ &=-\frac{1}{2\sigma^2}\sum_{n=1}^{N}(x_n-\mu)^2+\sum_{n=1}^{N}\ln(2\pi\sigma^2)^{-\frac{1}{2}}\\ &=-\frac{1}{2\sigma^2}\sum_{n=1}^{N}(x_n-\mu)^2-\frac{N}{2}\ln(2\pi)-\frac{N}{2}\ln\sigma^2 \end{split}\tag{1.54}\]

我们可以得到关于$\mu$最⼤似然解

\[\mu_{ML} = \frac{1}{N}\sum_{n=1}^{N} x_n \tag{1.55}\]

这是样本均值（sample mean），即观测值 ${x_n}$ 的均值。

类似地，关于 $\sigma^2$ 最⼤化函数（1.54）， 我们得到了⽅差的最⼤似然解

\[\sigma^2_{ML} = \frac{1}{N}\sum_{n=1}^{N}(x_n-\mu_{ML})^2 \tag{1.56}\]

这是关于样本均值 $\mu_{ML}$ 的样本⽅差（sample variance）。 注意， 我们要同时关于 $\mu$ 和 $\sigma^2$ 来最⼤化函数（1.54）， 但是在⾼斯分布的情况下， $\mu$ 的解和 $\sigma^2$ ⽆关， 因此我们可以⾸先估计公式 （1.55）然后使⽤这个结果来估计公式（1.56）。

最⼤似然⽅法系统化地低估了分布的⽅差。这是⼀种叫做偏移（bias）的现象的例⼦，与多项式曲线拟合问题中遇到的过拟合问题相关。

很容易证明

\[\mathbb{E}[\mu_{ML}]=\mu \tag{1.57}\] \[\mathbb{E}[\sigma^2_{ML}] =(\frac{N-1}{N})\sigma^2 \tag{1.58}\]

根据公式（1.58），下⾯的对于⽅差参数的估计是⽆偏的。

\[\tilde{\sigma}^2 = (\frac{N}{N-1})\sigma^2_{ML} = \frac{1}{N-1}\sum_{n=1}^{N}(x_n-\mu_{ML})^2\tag{1.59}\]

注意，当数据点的数量N增⼤时，最⼤似然解的偏移会变得不太严重， 并且在极限N→∞的情况下，⽅差的最⼤似然解与产⽣数据的分布的真实⽅差相等。

1.2.5 重新考察曲线拟合问题

曲线拟合问题的⽬标是能够根据N 个输⼊$x = (x_1 , \dots , x_N )^T$ 组成的数据集和它们对应的⽬标值$t = (t_1,\dots, t_N)^T$，在给出输⼊变量x的新值的情况下，对⽬标变量t进⾏预测。为了达到这个⽬的，我们要假定，给定x的值，对应的t值服从⾼斯分布，分布的均值为y(x, w) ，由公式（1.1）给出。

\[p(t\mid x,w,\beta) = \mathcal{N}(t \mid y(x,w,\beta^{-1})) \tag{1.60}\]

我们现在⽤训练数据 { x, t } ，通过最⼤似然⽅法，来决定未知参数 w 和 $\beta$ 的值。如果数据假定 从分布（1.60）中抽取，那么似然函数为

\[p(t\mid x,w,\beta) = \mathcal{N}(t_n \mid y(x,w,\beta^{-1})) \tag{1.61}\]

代入（1.46）得到对数似然函数

\[\ln p(t \mid x,w,\beta) =-\frac{\beta}{2}\sum_{n=1}^{N}\{y(x_n,w)-t_n\}^2-\frac{N}{2}\ln(2\pi)+\frac{N}{2}\ln\beta \tag{1.62}\]

对于确定 w 的问题来说，最⼤化似然函数等价于最⼩化由公式（1.2）$\displaystyle E(w) = \frac{1}{2} \sum^{N}_{n=1}{y(x_n,w)- tn}^2$ 定义的平⽅和误差函数。

因此，在⾼斯噪声的假设下，平⽅和误差函数是最⼤化似然函数的⼀个⾃然结果。

我们也可以使⽤最⼤似然⽅法来确定⾼斯条件分布的精度参数 $\beta$ 。 关于 $\beta$ 来最⼤化函数 （1.62）

\[\frac{1}{\beta_{ML}}=\frac{1}{N}\sum_{n=1}^{N}\{y(x_n,w)-t_w\}^2 \tag{1.63}\]

对新的x的值进⾏预测, 给出t的概率分布的预测分布（predictive distribution）来表⽰.
把最⼤似然参数代⼊公式（1.60）

\[p(t\mid x,w,\beta) = \mathcal{N}(t \mid y(x,w_{ML},\beta_{ML}^{-1})) \tag{1.64}\]

朝着贝叶斯的⽅法前进⼀步，引⼊在多项式系数 w 上的先验分布。考虑下⾯形式的⾼斯分布

\[p(w\mid\alpha)=\mathcal{N}(w\mid0,\alpha^{-1}I)=(\frac{\alpha}{2\pi})^{\frac{M+1}{2}}\exp\{-\frac{\alpha}{2}w^{T}w\} \tag{1.65}\]

其中 $\alpha$ 是分布的精度，M + 1是对于M 阶多项式的向量 w 的元素的总数。像 $\alpha$ 这样控制模型参数分布的参数，被称为超参数（hyperparameters）。

使⽤贝叶斯定理， w 的后验概率正⽐于先验分布和似然函数的乘积。

\[p(w\mid x,t,\alpha,\beta) \propto p(t \mid x,w,\beta)p(w\mid \alpha) \tag{1.66}\]

给定数据集， 我们现在通过寻找最可能的 w 值（即最⼤化后验概率）来确定 w 。这种技术被称为最⼤后验（maximum posterior），简称MAP。

取公式（1.66）的负对数，结合公式（1.62）和 公式（1.65），我们可以看到，最⼤化后验概率就是最⼩化下式： \(\frac{\beta}{2}\sum_{n=1}^{N}\{y(x_n,w)-t_n\}^2+\frac{\alpha}{2}w^Tw \tag{1.67}\)

因此我们看到最⼤化后验概率等价于最⼩化正则化的平⽅和误差函数（之前在公式（1.4）中提到），正则化参数为 λ =$\alpha$ / $\beta$ 。

1.2.6 贝叶斯曲线拟合

上一节我们还是引入了w，并对w进行估计，这不是完全的贝叶斯方法。这节我们对w积分，这是贝叶斯方法的核心。
我们希望的是应用训练集合(X,T)，在已知新的数据x的情况下得到目标值t的概率分布:

\[p(t\mid x,\mathbf{x},\mathrm{t})=\int p(t\mid x,w)p(w\mid \mathbf{x},\mathrm{t})\mathrm{d}w \tag{1.68}\]

这⾥，p(t \mid x, w) 由公式（1.60）给出， 并且我们省略了对于 $\alpha$ 和 $\beta$ 的依赖， 简化记号。 这⾥，p(w \mid x, t)是参数的后验分布，可以通过对公式（1.66）归⼀化得到。我们在3.3节将看到， 对于曲线拟合这样的问题，后验分布是⼀个⾼斯分布，可以解析地求出。类似地，公式（1.68）中的积分也可以解析地求解。因此，预测分布由⾼斯的形式给出

\[p(t\mid x,\mathbf{x},\mathrm{t})=\mathcal{N}(t\mid m(x),s^2(x)) \tag{1.69}\]

其中，均值和⽅差分别为

\[m(x)=\beta \phi(x)^TS\sum_{n=1}^{N}\phi(x_n)t_n \tag{1.70}\] \[s^2(x)=\beta^{-1}+\phi(x)^TS\phi(x) \tag{1.71}\]

这里矩阵S由下式给出

\[S^{-1}=\alpha I+\beta\sum_{n=1}^{N}\phi(x)\phi(x)^T \tag{1.72}\]

其中，I 是单位矩阵，向量 $\phi(x)$ 被定义为 $\phi_i(x) = x^i (i = 0, \dots , M)$。

贝叶斯线性回归: https://www.cnblogs.com/wacc/p/5495448.html

1.3 模型选择

我们训练出了很多模型，因为可能发生过拟合，我们需要正则化。也需要一个判断泛化性能好坏的标准。一般用一个未参与训练的测试集，进行交叉验证（cross validation）。

对所有模型的优劣求平均。如果留出的数据只有一个就是留一验证（leave-one-out）。但缺点：
1.训练次数随着分割的变细而增加，时间成本增加。
2.参数太多，参数的组合甚至是指数型增加，我们如何选择测试集。

我们模型是由训练数据而决定的，不是参数的选择而决定。

赤池信息准则AIC （akaike information criterion）：选择下⾯使这个量最⼤的模型

\[\ln p(D\mid w_{ML}) - M \tag{1.73}\]

这里的$ p(D\mid w_{ML}) $是最合适的对数似然函数，$ M $是模型中的可调节参数。
贝叶斯信息准则BIC（Bayesian information criterion）。

1.4 维度灾难

高维数据数据难区分。

推广到曲线拟合上。我们有D个输入变量，一个三阶多项式系数随着D的增加是幂增加。

\[y(x, w) = w_0 + \sum_{i=1}^Dw_ix_i + \sum_{i=1}^D\sum_{j=1}^Dw_{ij}x_ix_j\\ + \sum_{i=1}^D\sum_{j=1}^D\sum_{k=1}^Dw_{ijk}x_ix_jx_k \tag{1.74}\]

这里是系数的个数正比于$ D^3 $。M阶多项式就正比于$ D^M $了。

高维到底会产生什么效果。比方说一个D维空间的半径r=1的球体。$ r = 1 − \epsilon $和半径$r = 1 $之间的部分占球的总体积的百分比是多少。

\[V_D(r) = K_Dr^D \tag{1.75}\] \[\frac{V_D(1) - V_D(1-\epsilon)}{V_D(1)} = 1 - (1 - \epsilon)^D \tag{1.76}\]

因此，在高维空间中，一个球体的大部分体积都聚集在表面附近的薄球壳上!

1.5 决策论

假设我们有⼀个输⼊向量x和对应的⽬标值向量t，我们的⽬标是对于⼀个新的x值，预测t。联合概率分布p(x,t) 完整地总结了与这些变量相关的不确定性。从训练数据集中确定p(x,t)是 推断(inference) 问题的⼀个例⼦。

医学诊断，我们给病人拍了X光片，来诊断他是否得了癌症。 输入向量$ x $是X光片的像素的灰度值集合，输出变量$ t $表示病人患有癌症，记作类$ C_1 $或者不患癌症，记作类$ C_2 $。实际中，我们可能二元变量（如：$ t = 0 $来表示$ C_1 $类，$t = 1 $来表示$ C_2 $类）来表示。

希望得到$ p(C_k\mid x) $。使用贝叶斯方法这些概率可以表示为：

\[p(C_k\mid x) = \displaystyle\frac{p(x\mid C_k)p(C_k)}{p(x)} \tag{1.77}\]

$ p(C_1) $表示在拍X光片前病人患有癌症的概率，同样的，$ p(C_1\mid x) $表示获得X光片信息后使用贝叶斯定理修正的后验概率。

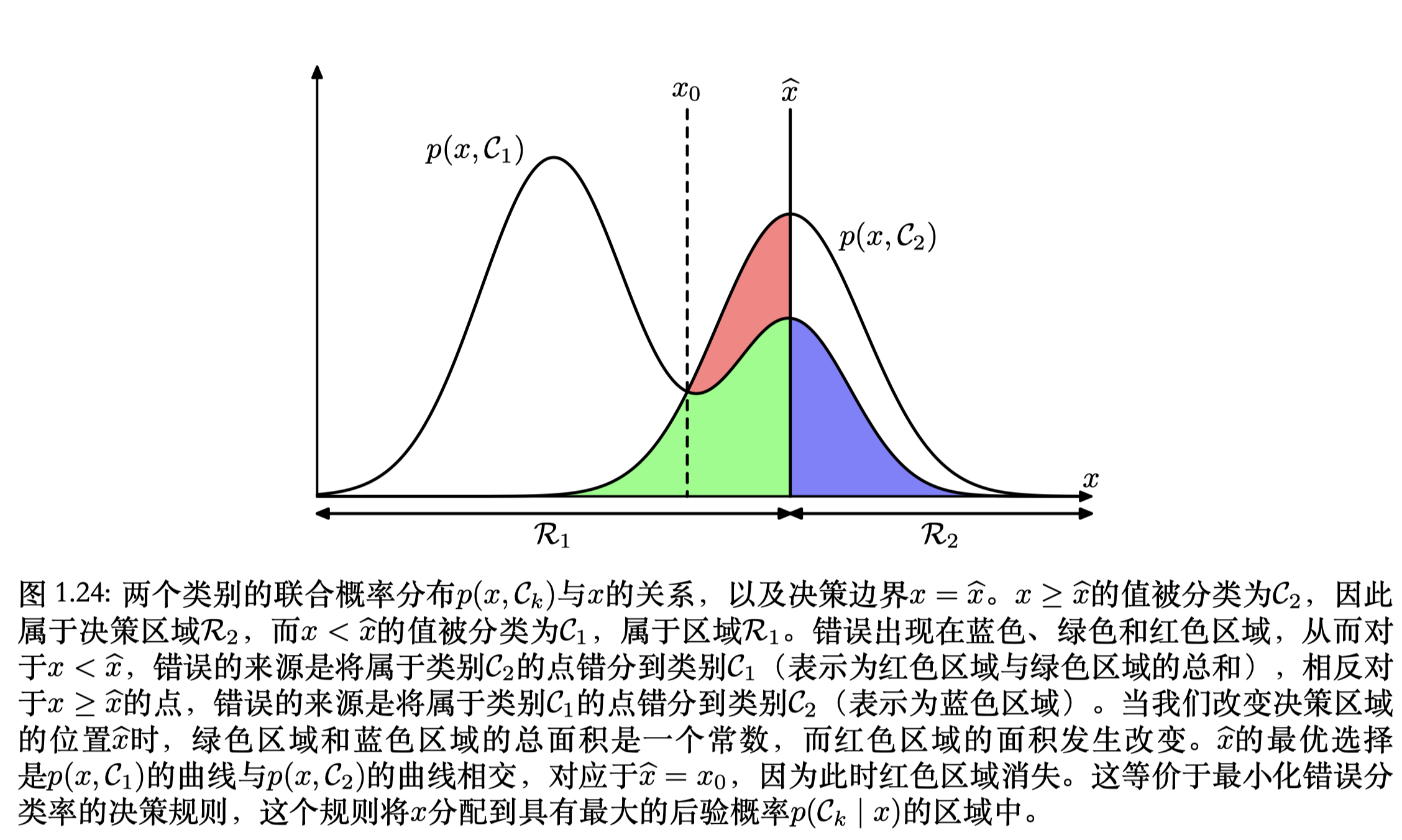
1.5.1 最⼩化错误分类率

假定我们的⽬标很简单，即尽可能少地作出错误分类。我们需要⼀个规则来把每个 x 的值分到⼀个合适的类别。这种规则将会把输⼊空间切分成不同的区域 Rk ，这种区域被称为决策区域 （decision region）。每个类别都有⼀个决策区域，区域 Rk 中的所有点都被分到 Ck 类。决策区域间的边界被叫做决策边界（decision boundary）或者决策⾯（decision surface）。

\[p(mistake) = p(x \in R_1, C_2) + p(x \in R_2, C_1) \\ = \int_{R_1} p(x, C_2)dx + \int_{R_2} p(x, C_1)dx \tag{1.78}\]

对于$ x $如果$p(x, C_1) > p(x, C_2) $，那么就把$ x $分到类$ C_1 $中。

对于更⼀般的K 类的情形，最⼤化正确率会稍微简单⼀些 \(p(\text{correct}) =\sum_{k=1}^{K} p(x\in\mathcal{R}_k ,\mathcal{C}_k) =\sum_{k=1}^{K}\int_{\mathcal{R}_k}p(x,\mathcal{C}_k)\mathrm{d}x\\ =\sum_{k=1}^{K}\int_{\mathcal{R}_k}p(\mathcal{C}_k\mid x)p(x)\mathrm{d}x \tag{1.79}\)

1.5.2 最⼩化期望损失

损失函数（loss function）也被称为代价函数（cost function），是对于所有可能的决策或者动作可能产⽣的损失的⼀种整体的度量。也可以考虑效⽤函数（utility function）

损失矩阵（loss matrix） 的第k, j个元素$L_{kj}$: 把真实类别$C_k$的 $x$ 分类为$C_j$的损失

最优解是使损失函数最⼩的解。平均损失根据这个联合概率分布p(x, C k )计算，定义为

\[\mathbb{E}[L]=\sum_k\sum_j \int_{R_j} L_{kj}p(x,C_k) \mathrm{d}x\tag{1.80}\]

优化⽬标是选择区域 $R_j$，来最⼩化期望损失。

使⽤乘积规则$p(x, C_k) = p(C_k\mid x)p(x)$ 来消除共同因⼦$p(x)$。决策规则: 对于每个新的$x$ ，把它分到第$j$类，能使下式取得最⼩值：

\[\sum_k L_{kj}p(C_k\mid x) \tag{1.81}\]

⼀旦我们知道了类的后验概率$p(C_k\mid x)$之后，这件事就很容易做了。

1.5.3 拒绝选项

在某些应⽤中，对于这种困难的情况，避免做出决策是更合适的选择。这样会使得模型的分类错误率降低。这被称为拒绝选项（reject option）.

1.5.4 推断和决策

直接将输⼊ x 直接映射为决策。这样的函数被称为判别函数（discriminant function）

三种⽅法：

• 生成模型（generative model）:通过对每个类别$C_k $，独立的确定类别的条件密度$ p(x \mid C_k) $来解决推断问题，还分别推断出类别的先验概率$　p(C_k) $，然后使用贝叶斯定理：

\[p(C_k\mid x) = \displaystyle\frac{p(x\mid C_k)p(C_k)}{p(x)} \tag{1.82}\]

来计算类别的后验概率$ p(C_k\mid x) $。

• 判别模型（discriminative models），解决确定类别的后验密度$p(C_k\mid x) $的推断问题，然后，使用决策论来对新的输入$ x $进行分类。

• 判别函数：找到能直接把输入$ x $映射到类别标签$ f(x) $。

使⽤后验概率来进⾏决策。这些理由包括：最⼩化风险,拒绝选项,补偿类先验概率,组合模型.

1.5.5 回归问题的损失函数

回到曲线拟合，计算平均损失，求期望。

\[\mathbb{E}[L] = \int\int L(t,y(x))p(x,t)dxdt \tag{1.86}\]

平方误差：

\[\mathbb{E}[L] = \int\int\{y(x) - t\}^2p(x, t)dxdt \tag{1.87}\]

变分法求解

\[\frac{\delta\mathbb{E}[L]}{\delta y(x)} = 2\int \{y(x) - t\}p(x,t)dt = 0 \tag{1.88}\]

整理：

\[y(x) = \frac{\int t p(x,t)dt}{p(x)} = \int t p(t\mid x)dt = \mathbb{E}_t[t\mid x] \tag{1.89}\]

这就是回归函数：条件$ x $下$ t $的条件均值

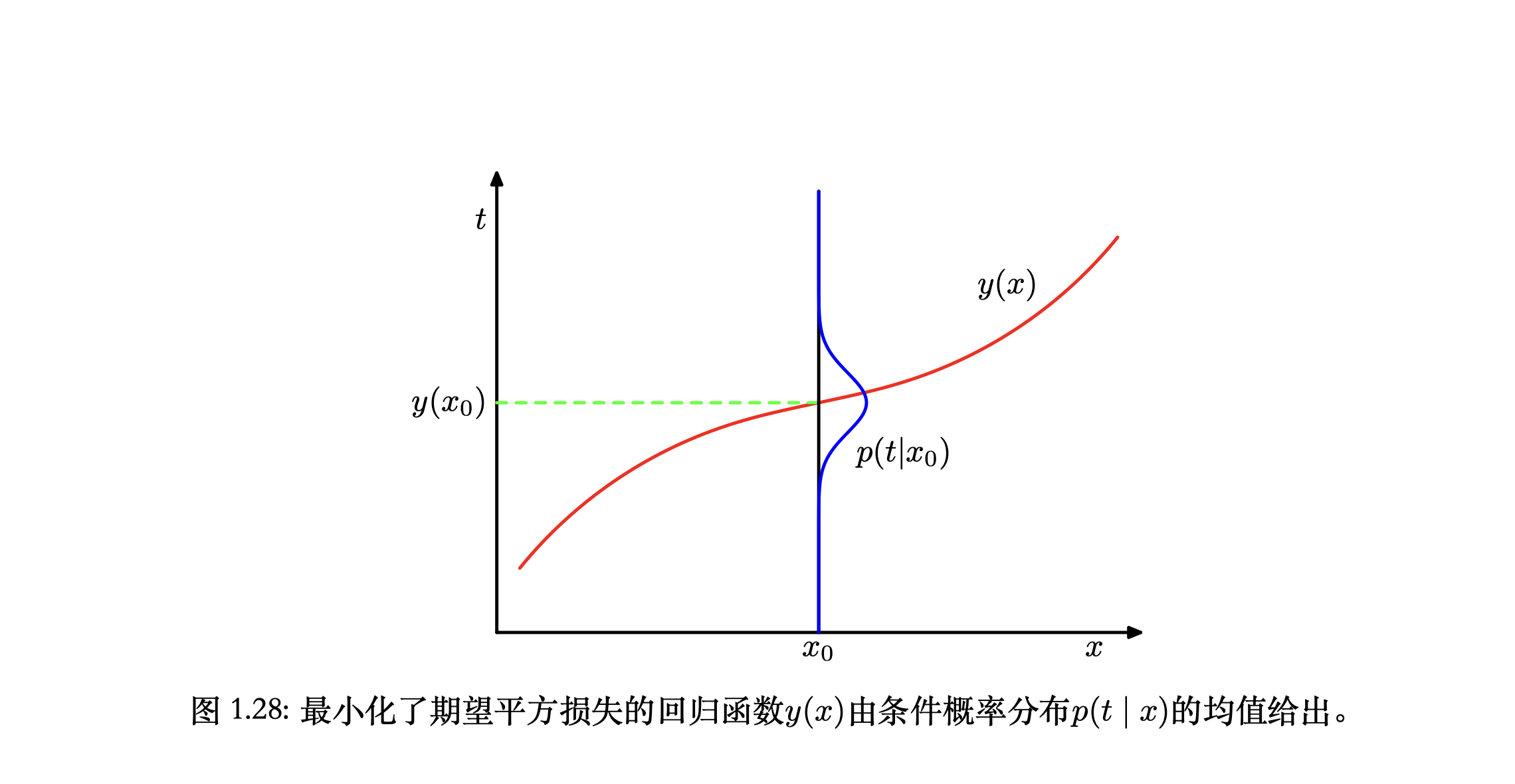
1.6 信息论

随机变量的熵:

\[H[x] = -\sum_{x}p(x)\log_2p(x)\]

⽆噪声编码定理（noiseless coding theorem）（Shannon, 1948）表明，熵是传输⼀个随机变量状态值所需的⽐特位的下界。

1.7 练习

1.1 解：

为求公式（1.2）最小化误差函数，将式（1.1）代入后，对$w_i$微分

\[\frac{\mathrm{d}E(w)}{\mathrm{d}w_i}=\sum_{n=1}^{N}\{[\sum_{j=0}^{M}w_jx_n^j-t_n]\}(x_n)^i\]

令导数为0，整理得到(1.122)

\[\sum_{j=0}^{M}\sum_{n=1}^{N}(x_n)^{i+j} w_j = \sum_{n=1}^{N}(x_n)^i t_n\]

1.2 解：

同理，对$\tilde{E}(w)$求导并令导数为0

\[\frac{\mathrm{d}\tilde{E}(w)}{\mathrm{d}w_i} = \sum_{n=1}^{N}\{[\sum_{j=0}^{M}w_jx_n^j-t_n]\}(x_n)^i+\lambda w_i = 0\]

整理得到

\[\sum_{j=0}^{M}[\sum_{n=1}^{N}(x_n)^{i+j}+\lambda I_{ij}] w_j = \sum_{n=1}^{N}(x_n)^i t_n\]

其中，$I_{ij}$ 在 $i=j$ 时为1，否则为0。

1.3 解：

事件记号按照单词的第一个字母命名。

根据全概率公式（1.13），选择苹果的边缘概率：

\[\begin{split} p(a)&=p(a\mid r)p(r)+ p(a\mid b)p(b)+ p(a\mid g)p(g)\\ &=0.2\times 0.3 + 0.2\times 0.5 + 0.6 \times 0.3 \\ &= 0.34 \end{split}\]

根据贝叶斯定理（1.12），选择的水果是橙色的，所选的盒子是绿色的概率：

\[\begin{split} p(g\mid o) &= \frac{p(o\mid g)p(g)}{p(o)}\\ &=\frac{p(o\mid g)p(g)}{p(o\mid r)p(r)+ p(o\mid b)p(b)+ p(o\mid g)p(g)}\\ &=\frac{0.6\times0.3}{0.6\times0.3+0.2\times0.4+0.2\times0.5}\\ &=0.5 \end{split}\]

1.4 解：

为了说明最大化$p_x(x)$对应的$\hat{x}$ 与最大化$p_y(y)$对应的$\hat{y}$ 并不一定按照简单的函数关系$\hat{x}=g(\hat{y})$相互对应，设$\mid g’(y)\mid =sg’(y),s\in[-1,1]$ ，然后对式（1.27）$p_y(y)=p_x(g(y))\mid g’(y)\mid $进行微分

\[p_y'(y)=sp'_x(g(y))[g'(y)]^2+sp_x(g(y))g''(y)\]

由于右侧第二项的存在，$\hat{x}=g(\hat{y})$不再成立，除非在线性变换的情况下，第二项被消去。

主要是说明了概率密度函数非线性变换之后的峰值是偏的。

1.5 解：

按照（1.38）方差的定义，把平⽅项展开， 我们看到⽅差也可以写成$f(x)$和$f(x)^2$ 的期望的形式（1.39）

\[\begin{split} \mathrm{var}(f(x)) &= \mathbb{E}[(f(x)-\mathbb{E}[f(x)])^2]\\ &=\mathbb{E}[f(x)^2-2f(x)\mathbb{E}[f(x)]+\mathbb{E}^2[f(x)]]\\ &=\mathbb{E}[f(x)^2]-2\mathbb{E}[f(x)]^2+\mathbb{E}[f(x)]^2\\ &=\mathbb{E}[f(x)^2]-\mathbb{E}[f(x)]^2 \end{split}\]

1.6 解：

当$x$与$y$独立时，$p(x,y)=p(x)p(y)$，对于离散情况

\[\begin{split} \mathbb{E}_{x,y}[xy]&=\sum_{x}\sum_{y}p(x,y)xy\\ &=\sum_{x}p(x)x\sum_{y}p(y)y\\ &=\mathbb{E}[x]\mathbb{E}[y] \end{split}\]

对于连续情况也有

\[\begin{split} \mathbb{E}_{x,y}[xy]&=\int_{x}\int_{y}p(x,y)xy\mathrm{d}x\mathrm{d}y\\ &=\int_{x}p(x)x\mathrm{d}x\int_{y}p(y)y\mathrm{d}y\\ &=\mathbb{E}[x]\mathbb{E}[y] \end{split}\]

按照协方差的定义有

\[\begin{split} \mathrm{cov}(x,y) &= \mathbb{E}_{xy}[\{x-\mathbb{E}[x]\}\{y-\mathbb{E}[y]\}]\\ &=\mathbb{E}_{xy}[xy-x\mathbb{E}[y]-y\mathbb{E}[x]+\mathbb{E}[x]\mathbb{E}[y]]\\ &=\mathbb{E}_{xy}[xy]-\mathbb{E}[x]\mathbb{E}[y]-\mathbb{E}[x]\mathbb{E}[y]+\mathbb{E}[x]\mathbb{E}[y]\\ &=\mathbb{E}_{xy}[xy]-\mathbb{E}[x]\mathbb{E}[y]\\ &=0 \end{split}\]

1.7 解：

\[\begin{split} I^2 &=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\exp(\frac{1}{2\sigma^2}x^2)\mathrm{d}x\\ &= \int_0^{\infty}\int_0^{2\pi}\exp(-\frac{r^2}{2\sigma^2})r\mathrm{d}\theta\mathrm{d}r\\ &=2\pi\int_0^{\infty}\exp(-\frac{r^2}{2\sigma^2})r \mathrm{d}r\\ &=-2\sigma^2\pi\int_0^{\infty}\exp(-\frac{u}{2\sigma^2})\mathrm{d}(-\frac{u}{2\sigma^2})\\&=2\pi\sigma^2 \end{split}\]

因此，$I = (2\pi\sigma^2)^{1/2}$。

1.8 解：

令 $y=x-\mu$,

\[\begin{split} \mathbb{E}[x]&=\int_{-\infty}^{\infty}\mathcal{N}\left(x \mid \mu, \sigma^{2}\right)x\mathrm{d}x\\ &=\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \int_{-\infty}^{\infty}\exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\}x\mathrm{d}x\\ &=\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \int_{-\infty}^{\infty}\exp \left\{-\frac{y^{2}}{2 \sigma^{2}}\right\}(y+\mu)\mathrm{d}y\\ &=\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \int_{-\infty}^{\infty}\exp \left\{-\frac{y^{2}}{2 \sigma^{2}}\right\}y\mathrm{d}y + \frac{\mu}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}}\int_{-\infty}^{\infty}\exp \left\{-\frac{y^{2}}{2 \sigma^{2}}\right\}\mathrm{d}y \end{split}\]

由于第一项是奇函数，积分为0，第二项是$\mu$乘以一个正态分布的积分，结果为$\mu$，因此$\mathbb{E}[x]=\mu$。

由（1.127）

\[\int_{-\infty}^{\infty}\mathcal{N}(x \mid \mu, \sigma^{2})\mathrm{d}x=1\]

得到

\[\int_{-\infty}^{\infty}\exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\}\mathrm{d}x=\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}\]

两边对$\sigma^2$微分，整理得到

\[\int_{-\infty}^{\infty} \left(\frac{1}{2 \pi \sigma^{2}}\right)^{\frac{1}{2}} \exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\}(x-\mu)^{2}\mathrm{d}x=\sigma^{2}\]

即正态分布方差公式

\[\mathbb{E}[(x-\mu)^2]=\sigma^2\]

整理得

\[\mathbb{E}[x^2]-2\mu\mathbb{E}[x]+\mu^2=\sigma^2\\\] \[\mathbb{E}[x^2]=\sigma^2+\mu^2\]

所以

\[\mathbb{E}[x^2]-\mathbb{E}[x]^2=\sigma^2\]

1.9 解：

\[\frac{\mathrm{d}}{\mathrm{d}x}\mathcal{N}(x\mid\mu,\sigma^2)=-\mathcal{N}(x\mid\mu,\sigma^2)\frac{x-\mu}{\sigma^2}\]

由于$\mathcal{N}(x\mid\mu,\sigma^2)$非负，因此最大值在 $x=\mu$ 取到。

\[\begin{split} \frac{\partial}{\partial\mathbf{x}}\mathcal{N}(\mathbf{x}\mid\mathbf{\mu},\mathbf{\Sigma})=-\mathcal{N}(\mathbf{x}\mid\mathbf{\mu},\mathbf{\Sigma})\mathbf{\Sigma}^{-1}(\mathbf{x}-\mathbf{\mu}) \end{split}\]

同样，最大值在 $x=\mu$ 取到。

1.10 解：

由于 $x,z$ 相互独立，因此 $p(x,z)=p(x)p(z)$

\[\begin{split} \mathbb{E}[x+z]&=\int\int (x+z)p(x)p(z)\mathrm{d}x\mathrm{d}z\\ &=\int p(z)\mathrm{d}z\int xp(x)\mathrm{d}x+\int p(x)\mathrm{d}x\int zp(z)\mathrm{d}z\\ &=\int xp(x)\mathrm{d}x + \int zp(z)\mathrm{d}z = \mathbb{E}[x]+\mathbb{E}[z] \end{split}\] \[\begin{split} \mathrm{var}[x+z]&=\int \int (x+z-\mathbb{E}[x+z])^2 p(x)p(z)\mathrm{d}x\mathrm{d}z\\ &=\int \int\left[(x-\mathbb{E}[x])^2-2(x-\mathbb{E}[x])(z-\mathbb{E}[z])+(z-\mathbb{E}[z])^2 \right]p(x)p(z)\mathrm{d}x\mathrm{d}z\\ &=\int(x-\mathbb{E}[x])^2p(x)\mathrm{d}x+\int(z-\mathbb{E}[z])p(z)\mathrm{d}z=\mathrm{var}[x]+\mathrm{var}[z] \end{split}\]

1.11 解：令公式(1.54)导数为0可得

1.12 解：

根据公式（1.55）

\[\mathbb{E}[\mu_{ML}]=\mathbb{E}\left[ \frac{1}{N}\sum_{n=1}^{N}x_n \right]=\mu\]

将（1.55）代入（1.56），运用题干性质

\[\begin{split} \mathbb{E}[\sigma^2_{ML}] &= \mathbb{E}\left[\frac{1}{N}\sum_{n=1}^{N} \left(x_n-\frac{1}{N}\sum_{m=1}^{N}x_m \right)^2\right]\\ &=\frac{1}{N}\sum_{n=1}^{N} \mathbb{E} \left[ x_n^2-2x_n\frac{1}{N}\sum_{m=1}^{N}x_m + \frac{1}{N^2}\sum_{m=1}^{N}\sum_{l=1}^{N}x_l x_m\right]\\ &=\mu^2+\sigma^2-\frac{2}{N}\left(\mu^2+\sigma^2+(N-1)\mu^2\right)\\ &\ \ \ \ \ +\frac{1}{N^2}\left(N(\mu^2+\sigma^2)+N(N-1)\mu^2\right) \\&=\left(\frac{N-1}{N} \right)\sigma^2 \end{split}\]

1.13 解：

\[\frac{1}{N}\sum_{n=1}^{N}\mathbb{E}[(x_n-\mu)^2]\\ =\frac{1}{N}\sum_{n=1}^{N}\mathbb{E}[x_n^2-2x_n\mu+\mu^2]\\ =(\mu^2+\sigma^2)-2\mu^2+\mu^2\\ =\sigma^2\]

1.14 解：

定义

\[w_{ij}^S=\frac{1}{2}(w_{ij}+w_{ji})\\ w_{ij}^A=\frac{1}{2}(w_{ij}-w_{ji})\]

有 $w_{ij}=w^S_{ij}+w^A_{ij}$

由于

\[\sum_{i=1}^N\sum_{j=1}^N w^A_{ij}x_ix_j=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N(w_{ij}-w_{ji})x_ix_j=0\]

因此有

\[\sum_{i=1}^N\sum_{j=1}^N w_{ij}x_ix_j = \sum_{i=1}^N\sum_{j=1}^N (w^A_{ij}+w^S_{ij})x_ix_j=\sum_{i=1}^N\sum_{j=1}^N w^S_{ij}x_ix_j\]

我们看到，不失⼀般性，系数$w_{ij}$的矩阵可以选择成对称的，因此独立参数由对角线上的元素和一半非对角线上的元素组成，总个数为$D+(D^2-D)/2 = D(D+1)/2$.

1.15 解：

1.17 解：

\[\Gamma(x) \equiv \int_0^\infty u^{x-1}e^{-u}\mathrm{d}u\]

证明Gamma 函数的性质

\[\Gamma(x+1)=\int_0^\infty u^xe^{-u}\mathrm{d}u= \int_0^\infty u^x\mathrm{d}(-e^{-u}) \\ =u^x(-e^{-u})\mid^{\infty}_{0} - \int_0^{\infty} -e^{-u} \mathrm{d}u^x \\ = (0-0) - \int_0^{\infty} -e^{-u} xu^{x-1}\mathrm{d}u = x\Gamma (x)\] \[\Gamma(1)= \int_0^\infty u^0 e^{-u}\mathrm{d}u = (-e^{-u}) \mid_0^\infty = 0-(-1)=1\]

$x \in \mathbb{Z}，x\ge1$ 时有

\[\Gamma(x+1)= x\Gamma (x) = x(x-1)\Gamma (x-1) = \dots = x!\Gamma(1)=x!\]