PRML笔记 Ch2.概率密度函数 - Zhihan's Blogs

密度估计（density estimation）：给定有限次观测$x_1,\dots,x_N$ 的前提下，对随机变量x的概率分布$p(x)$建模。

参数分布（parametric distribution）：少量可调节的参数控制了整个概率分布。

2.1 二元变量

伯努利分布

考虑一个二元随机变量$x\in{0,1}$，$x=1$的概率被记作参数$\mu$，$x$的概率分布为伯努利分布（Bernoulli distribution）

\[\mathrm{Bern}(x\mid\mu)=\mu^x(1-\mu)^{1-x} \tag{2.2}\]

model = Bernoulli()
model.fit(np.array([0., 1., 1., 1.]))
print(model)

Bernoulli(
    mu=0.75
)

二项分布

假设有一个$x$的观测值的数据集$\mathcal{D}={x_1,\dots,x_N}$。可以构造关于$\mu$的似然函数如下

\[p(\mathcal{D} \mid \mu) = \prod_{n=1}^N p(x_n\mid \mu)=\prod_{n=1}^N \mu^{x_n}(1-\mu)^{1-x_n} \tag{2.5}\]

给定数据集规模$N$的条件下，$x=1$ 的观测出现的数量$m$的概率分布，这被称为二项分布（binomial distribution）。为了得到归一化系数，我们注意到，在$N$次抛掷中，我们必须把所有获得$m$个正面朝上的方式都加起来，因此二项分布可以写成

\[\mathrm{Bin}(m\mid N,\mu)=\frac{N!}{(N-m)!m!}\mu^m(1-\mu)^{N-m} \tag{2.9}\]

期望：

\[\mathbb{E}[\mu]=\displaystyle\frac{a}{a+b}\tag{2.3}\]

方差：

\[\mathbb{E}[\mu^2] = \displaystyle\frac{ab}{(a+b+1)(a+b)^2}\tag{2.4}\]

参数$a$和$b$经常被称为超参数（hyperparameter），因为它们控制了参数$\mu$的概率分布。

数据集$D = { x_1,… , x_N}$是从$p(x\mid \mu)$中抽取的，构造关于$\mu$的似然函数

\[p(D\mid \mu) = \prod\limits_{n=1}^Np(x_n\mid \mu) = \prod\limits_{n=1}^{N}\mu^{x_n}(1-\mu)^{1-x_n} \tag{2.5}\]

最大化对数似然

\[\ln p(D\mid \mu) = \sum\limits_{n=1}^N\ln p(x_n\mid \mu) = \sum\limits_{n=1}^N{x_n\ln \mu + (1 - x_n)\ln(1-\mu)} \tag{2.6}\]

这个只用N次观测结果得到的似然函数，也叫充分统计量。令其导数为零，我们有最大似然的估计值时的$\mu$:1

\[\mu_{ML} = \frac{1}{N}\sum\limits_{n=1}^N x_n \tag{2.7}\]

这也叫做样本均值。如果把x=1的观测次数记录为m，则2.7可以写成：

\[\mu_{ML} = \frac{m}{N} \tag{2.8}\]

求解$N$次抛掷中$m$次朝上的次数

\[\mathrm{Bin}(m\mid N,\mu) = C_M^N \mu^m (1-\mu)^{N-m} \tag{2.9}\]

其中，

\[C_M^N = \displaystyle\frac{N!}{(N-m)!m!}\tag{2.10}\]

均值

\[\mathbb{E}[m] = \sum_{m=0}^N m \mathrm{Bin}(m\mid N,\mu) = N\mu \tag{2.11}\]

方差

\[\mathrm{var}[m]= \sum_{m=0}^N (m-\mathrm{var}[m])^2 \mathrm{Bin}(m\mid N,\mu) = N\mu(1-\mu) \tag{2.12}\]

2.1.1 Beta分布

注意到似然函数（2.5）是某个因子与$\mu^x(1-\mu)^{1-x}$乘积的形式。如果我们选择一个正比于$\mu$和$(1-\mu)$的幂指数的先验概率分布，那么后验概率分布就会有着与先验分布相同的函数形式。这个性质被叫做共轭性（conjugacy）。

因此，我们把先验分布选择为Beta分布，定义为

\[\mathrm{Beta}(\mu\mid a,b) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1}\tag{2.13}\]

其中

\[\Gamma(x) \equiv \int_0^\infty u^{x-1}e^{-u}\mathrm{d}u\]

Beta分布归一化证明：

\[\begin{split} 即证： \frac{\Gamma(a)\Gamma(b)} {\Gamma(a+b)} &= \int_{-\infty}^{\infty}\mu^{a-1}(1-\mu)^{b-1} \mathrm{d}\mu \\ \Gamma(a)\Gamma(b)&= \int_0^{\infty} e^{-x}x^{a-1}\mathrm{d}x \int_0^{\infty}e^{-y}y^{b-1}\mathrm{d}y \\ &=\int_0^{\infty} \int_0^{\infty} x^{a-1}y^{b-1}e^{-(x+y)} \mathrm{d}y\mathrm{d}x \end{split}\]

令$t=x+y$,则$\mathrm{d}y=\mathrm{d}t,t\in(x,\infty)$

\[\begin{split} \\ &=\int_0^{\infty}\int_x^{\infty} x^{a-1}(t-x)^{b-1}e^{-t}\mathrm{d}t\mathrm{d}x \\ &=\int_0^\infty \int_0^t x^{a-1}(t-x)^{b-1} e^{-t} \mathrm{d}x\mathrm{d}t \end{split}\]

令$x=t\mu,x\in(0,t)$,则$\mu\in(0,1),\mathrm{d}x=t\mathrm{d\mu}$

\[\begin{split} &=\int_0^{\infty} \int_0^1(t\mu)^{a-1}(t-t\mu)^{b-1}e^{-t}t\mathrm{d}\mu \mathrm{d}t \\ &=\int_0^\infty \int_0^1 \mu^{a-1}(1-\mu)^{b-1} \mathrm{d}\mu \mathrm{d}t \\ &=\int_0^\infty t^{a+b-1}e^{-t}\mathrm{d}t \int_0^1 \mu^{a-1}(1-\mu)^{b-1} \mathrm{d}\mu \\ &=\Gamma(a+b)\int_{-\infty}^{\infty}\mu^{a-1}(1-\mu)^{b-1} \mathrm{d}\mu \end{split}\]

Beta分布期望证明：

\[\begin{split} \mathbb{E}[\mu]&=\int_0^1 \mu \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1} \mathrm{d}\mu\\ &=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\int_0^1 \mu^{a}(1-\mu)^{b-1} \mathrm{d}\mu\\ &=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\cdot \frac{\Gamma(a+1)\Gamma(b)}{\Gamma(a+b+1)} \\ &=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\cdot \frac{a\Gamma(a)\Gamma(b)}{(a+b)\Gamma(a+b)}\quad(\text{习题1.17})\\ &=\frac{a}{a+b} \end{split}\]

Beta分布方差证明：

\[\begin{split} \mathbb{E}[\mu^2]&=\int_0^1 \mu^2 \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1} \mathrm{d}\mu\\ &=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\int_0^1 \mu^{a+1}(1-\mu)^{b-1} \mathrm{d}\mu\\ &=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\cdot \frac{\Gamma(a+2)\Gamma(b)}{\Gamma(a+b+2)}\\ &=\frac{(a+1)a}{(a+b+1)(a+b)}\\ \mathrm{var}[\mu]&=\mathbb{E}[\mu^2]-\mathbb{E}[\mu]^2 \\ &= \frac{ab}{(a+b+1)(a+b)^2} \end{split}\]

# 图 2.2: 对于不同的超参数a和b，公式（2.13）给出的Beta分布不同超参数对应图
x = np.linspace(0, 1, 100)
for i, [a, b] in enumerate([[0.1, 0.1], [1, 1], [2, 3], [8, 4]]):
    plt.subplot(2, 2, i + 1)
    beta = Beta(a, b)
    plt.xlim(0, 1)
    plt.ylim(0, 3)
    plt.plot(x, beta.pdf(x))
    plt.annotate("a={}".format(a), (0.1, 2.5))
    plt.annotate("b={}".format(b), (0.1, 2.1))
plt.show()

svg

$\mu$ 的后验概率分布可以这样得到：Beta先验与二项似然函数相乘，只保留依赖$\mu$的因子，后验概率分布的形式为

\[p(\mu \mid m,l,a,b) \propto \mu^{m+a-1} (1-\mu)^{l+b-1} \tag{2.17}\]

其中 $l$ 对应样本 $x=0$ 的数量，通过对比二项分布的形式可以得到归一化系数

\[p(\mu \mid m,l,a,b) = \frac{\Gamma(m+a+l+b)}{\Gamma(m+a)\Gamma(l+b)}\mu^{m+a-1}(1-\mu)^{l+b-1}\\ = \mathrm{Beta}(\mu\mid m+a,l+b) \tag{2.18}\]

这反映出先验关于似然函数的共轭性质。

#图2.3 贝叶斯顺序推断

beta = Beta(2, 2)
plt.subplot(2, 1, 1)
plt.xlim(0, 1)
plt.ylim(0, 2)
plt.plot(x, beta.pdf(x))
plt.annotate("prior", (0.1, 1.5))


model = Bernoulli(mu=beta)
model.fit(np.array([1]))
plt.subplot(2, 1, 2)
plt.xlim(0, 1)
plt.ylim(0, 2)
plt.plot(x, model.mu.pdf(x))
plt.annotate("posterior", (0.1, 1.5))

plt.show()

svg

顺序（sequential）方法：每次使用一个观测值，或者每次使用一小批观测值。在数据集⽆限⼤的极限情况下，此时公式（2.20）的结果变成了最⼤似然的结果（2.8）

随着我们观测到越来越多的数据，后验概率表示的不确定性将会持续下降。用频率学家的观点考虑贝叶斯学习问题,参数为$\theta$，并且我们观测到了一个数据集$\mathcal{D}$，由联合概率分布$p(\theta,\mathcal{D})$描述，有如下性质

\[\mathbb{E}_\theta[\theta]= \mathbb{E}_{D}[\mathbb{E}_\theta[\theta\mid D]] \tag{2.21}\]

其中

\[\mathbb{E}_\theta[\theta]= \int p(\theta)\theta \mathrm{d}\theta \tag{2.22}\] \[\mathbb{E}_{D}[\mathbb{E}_\theta[\theta\mid D]] =\int \left\{ \int \theta p(\theta \mid D) \mathrm{d} \theta \right\} \mathrm{d} D \tag{2.23}\]

表明， θ 的后验均值，在产⽣数据集的整个分布上⾯做平均，等于 θ 的先验均值。类似可证

\[\mathrm{var}_\theta [\theta] = E_D [\mathrm{var} [\theta \mid D]] + \mathrm{var}_D [E_\theta [\theta \mid D]] \tag{2.24}\]

2.2 多项式变量

多项式变量：$K$维向量$\boldsymbol{x}$中的一个元素$x_k=1$，其余元素均为0，例如

\[x = (0, 0, 1, 0, 0, 0)^T \tag{2.25}\]

如果用$\mu_k$表示$x_k=1$的概率，那么$\boldsymbol{x}$ 的分布就是

\[p(\boldsymbol{x} \mid \boldsymbol{\mu}) = \prod_{k=1}^{K}\mu_k^{x_k} \tag{2.26}\]

参数$\mu_k$要满⾜ $\mu_k \ge 1$和$\sum_k \mu_k =1$。上式是归一化的，可看成伯努利分布的多输出推广。

现在考虑一个有$N$个独立观测值$\boldsymbol{x}_1,\dots,\boldsymbol{x}_N$ 的数据集$\mathcal{D}$。对应的似然函数的形式为

\[p(\mathcal{D} \mid \boldsymbol{\mu})=\prod_{n=1}^{N} \prod_{k=1}^{K} \mu_{k}^{x_{n k}}=\prod_{k=1}^{K} \mu_{k}^{\left(\sum_{n} x_{n k}\right)}=\prod_{k=1}^{K} \mu_{k}^{m_{k}} \tag{2.29}\]

$m_k=\sum_n x_{nk}（2.30）$表示观测到$x_k=1$的次数，被称为这个分布的充分统计量（sufficient statistics）。

求最大似然解，需要在约束$\sum_k \mu_k =1$下关于$\mu_k$最大化$\ln(p(\mathcal{D}\mid \boldsymbol{\mu}))$ 。运用拉格朗日乘数法 $L = \sum_{k=1}^Km_k\ln \mu_k + \lambda \left(\sum_{k=1}^K \mu_k -1\right) \tag{2.31}$

\[\frac{\partial L}{\partial \mu_k} = \frac{m_k}{\mu_k}+\lambda = 0\] \[\mu_k = -\frac{m_k}{\lambda} \tag{2.32}\]

$（2.32）$代入约束$\sum_k \mu_k =1$，可得

\[-\frac{\sum_k m_k}{\lambda} = -\frac{N}{\lambda}=1, \lambda = -N\]

所以最大似然解为

\[\mu_k^{ML}=\frac{m_k}{N}\]

多项式分布（multinomial distribution）

考虑$m_1,\dots,m_K$在参数$\boldsymbol{\mu}$和观测总数$N$条件下的联合分布。根据公式（2.29），

\[\mathrm{Mult}(m_1,m_2,\dots,m_K \mid \boldsymbol{\mu},N)= \frac{N!}{m_1!m_2!\dots m_K!}\prod_{k=1}^{K} \mu_k^{m_k} \tag{2.34}\]

归一化系数是把$N$个物体分成大小为$m_1,\dots,m_K$的$K$组的方案总数。

2.2.1 狄利克雷分布

多项式分布（2.34）的参数{$\mu_k$}的一组先验分布。多项式分布的共轭先验

\[p(\boldsymbol{\mu\mid \alpha}) \propto \prod_{k=1}^{K} \mu_k^{\alpha_k-1} \tag{2.37}\]

其中$0\le \mu \le 1$且$\sum_k\mu_k =1$， $\boldsymbol{\alpha}=(\alpha_1,\dots,\alpha_K)^T$ 是分布的参数。

由于加和的限制，${\mu_k}$空间上的分布被限制在K-1维的单纯形（simplex）当中。

# 图2.4 单纯形
fig, ax = plt.subplots(figsize=(3, 3))
d = plt.imread('./graph/figure2.4.png')
plt.axis('off')
ax.imshow(d)

svg

归一化得到：（习题2.9归纳法）

\[\mathrm{Dir}(\boldsymbol{\mu\mid \alpha}) = \frac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)\cdots\Gamma(\alpha_K)} \prod_{k=1}^{K} \mu_k^{\alpha_k-1} \tag{2.38}\]

其中

\[\alpha_0=\sum_{k=1}^K \alpha_k \tag{2.39}\]

似然函数（2.34）乘以先验（2.38）得到参数${\mu_k}$的后验分布，形式为

\[p(\boldsymbol{\mu} \mid \mathcal{D},\boldsymbol{\alpha})\propto p(\mathcal{D} \mid \boldsymbol{\mu})p(\boldsymbol{\mu\mid \alpha}) \propto \prod_{k=1}^K \mu_k^{\alpha_k+m_k-1} \tag{2.40}\]

比较（2.38）确定归一化系数

\[p(\boldsymbol{\mu} \mid \mathcal{D},\boldsymbol{\alpha}) = \mathrm{Dir}(\boldsymbol{\mu}\mid\boldsymbol{\alpha}+\boldsymbol{m}) \\ =\frac{\Gamma(\alpha_0+N)}{\Gamma(\alpha_1+m_1)\cdots\Gamma(\alpha_K+m_K)} \prod_{k=1}^{K} \mu_k^{\alpha_k+m_k-1} \tag{2.41}\]

其中，$\boldsymbol{m}=(m_1,\dots,m_K)^T$。

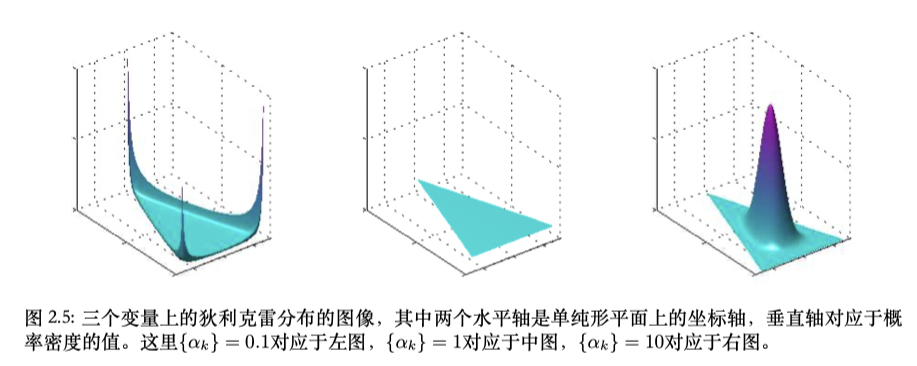
2.3 高斯分布

一元高斯分布

\[\mathcal{N}\left(x \mid \mu, \sigma^{2}\right)=\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\} \tag{2.42}\]

其中 $\mu$ 是均值, $\sigma^{2}$ 是方差。

多元高斯分布

\[\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{(2 \pi)^{\frac{D}{2}}} \frac{1}{\mid \boldsymbol{\Sigma}\mid ^{\frac{1}{2}}} \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\} \tag{2.43}\]

其中, $\boldsymbol{\mu}$ 是一个 $D$ 维均值向量, $\boldsymbol{\Sigma}$ 是一个 $D \times D$ 的协方差矩阵, $\mid \boldsymbol{\Sigma}\mid $ 是 $\boldsymbol{\Sigma}$ 的行列式。

高斯分布的几何形式

二次型

\[\Delta^{2}=(\boldsymbol{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \tag{2.44}\]

$\Delta$ 被叫做 $\mu$ 和 $x$ 之间的马氏距离（Mahalanobis distance）。当 $\Sigma$ 是单位矩阵时就是欧式距离。 $x$ 空间中这个二次型是常数曲面, 高斯分布是常数。

矩阵 $\Sigma$ 可以取为对称矩阵, 而不失一般性。这是因为任何非对称项都会从指数中消失。(为什么？证明：习题2.17)

协方差矩阵的特征向量方程 $\boldsymbol{\Sigma u_i}=\lambda_{i} \boldsymbol{u}_{i} \tag{2.45}$

其中 $i=1, \ldots, D$ 。由于 $\boldsymbol{\Sigma}$ 是实对称矩阵, 因此它的特征值也是实数，证明如下。

特征值是实数的证明：

特征向量⽅程的定义为

\[\boldsymbol{A} \boldsymbol{u}_{i}=\lambda_{i} \boldsymbol{u}_{i} \tag{C.29}\]

首先将定义式左乘 $\left(\boldsymbol{u}_{i}^{*}\right)^{T}$, 其中 $*$ 表示复共轭

\[\left(\boldsymbol{u}^{*}_{i}\right)^{T} \boldsymbol{A} \boldsymbol{u}_{i}=\lambda_{i}\left(\boldsymbol{u}_{i}^{*}\right)^{T} \boldsymbol{u}_{i} \tag{C.30}\]

对定义式取复共轭, 然后左乘 $\boldsymbol{u}_{i}^{T}$, 可得

\[\boldsymbol{u}_{i}^{T} \boldsymbol{A} \boldsymbol{u}_{i}^{*}=\lambda_{i}^{*} \boldsymbol{u}_{i}^{T} \boldsymbol{u}_{i}^{*} \tag{C.31}\]

推导过程中, 我们使用了 $\boldsymbol{A}^{*}=\boldsymbol{A}$, 因为我们只考虑实对称矩阵 $\boldsymbol{A}$ 。

将第二个方程取转置,

\[\left(\boldsymbol{u}^{*}_{i}\right)^{T} \boldsymbol{A}^{T} \boldsymbol{u}_{i}=\lambda_{i}^{*} \left(\boldsymbol{u}_{i}^{*}\right)^{T} \boldsymbol{u}_{i}\]

使用 $\boldsymbol{A}^{T}=\boldsymbol{A}$, 我们看到两个方程的左侧相同, 从而 $\lambda_{i}^{*}=\lambda_{i}$, 因此 $\lambda_{i}$ 一定是实数。

特征向量可以被选成单位正交的, 即

\[\boldsymbol{u}_{i}^{T} \boldsymbol{u}_{j}=I_{i j} \tag{2.46}\]

其中 $I_{i j}$ 是单位矩阵 $\boldsymbol{I}$ 的第 $i, j$ 个元素, 满足

\[I_{i j}= \begin{cases}1, & \text { 如果 } i=j \\ 0, & \text { 其他情况 }\end{cases} \tag{2.47}\]

特征向量正交性证明：

我们首先将公式 (C.29) 左乘 $\boldsymbol{u}_{j}^{T}$, 得到

\[\boldsymbol{u}_{j}^{T} \boldsymbol{A} \boldsymbol{u}_{i}=\lambda_{i} \boldsymbol{u}_{j}^{T} \boldsymbol{u}_{i} \tag{C.34}\]

因此, 通过交换下标, 我们有

\[\boldsymbol{u}_{i}^{T} \boldsymbol{A} \boldsymbol{u}_{j}=\lambda_{j} \boldsymbol{u}_{i}^{T} \boldsymbol{u}_{j} \tag{C.35}\]

我们现在对(C.35)取转置, 使用对称性质 $\boldsymbol{A}^{T}=\boldsymbol{A}$, 然后将两个方程相减, 可得

\[\left(\lambda_{i}-\lambda_{j}\right) \boldsymbol{u}_{i}^{T} \boldsymbol{u}_{j}=0 \tag{C.36}\]

因此, 对于 $\lambda_{i} \neq \lambda_{j}$, 我们有 $\boldsymbol{u}_{i}^{T} \boldsymbol{u}_{j}=0$, 因此 $\boldsymbol{u}_{i}$ 和 $\boldsymbol{u}_{j}$ 是正交的。如果两个特征值是相等的, 那么任意线性组合 $\alpha \boldsymbol{u}_{i} + \beta \boldsymbol{u}_{j}$ 也是一个有着相同特征值的特征向量, 因此我们可以任意选择一个线性组合, 然后选择第二个特征向量正交于第一个（可以证明这种退化的特征向量永远不会线性相关）。

协方差矩阵 $\boldsymbol{\Sigma}$ 可以表示成特征向量的展开的形式

\[\boldsymbol{\Sigma}=\sum_{i=1}^{D} \lambda_{i} \boldsymbol{u}_{i} \boldsymbol{u}_{i}^{T} \tag{2.48}\]

类似地, 协方差矩阵的逆矩阵 $\boldsymbol{\Sigma}^{-1}$ 可以表示为

\[\boldsymbol{\Sigma}^{-1}=\sum_{i=1}^{D} \frac{1}{\lambda_{i}} \boldsymbol{u}_{i} \boldsymbol{u}_{i}^{T} \tag{2.49}\]

把公式 $(2.49)$ 代入公式 $(2.44)$，二次型就变成了

\[\Delta^{2}=\sum_{i=1}^{D} \frac{y_{i}^{2}}{\lambda_{i}} \tag{2.50}\]

其中我们定义

\[y_{i}=\boldsymbol{u}_{i}^{T}(\boldsymbol{x}-\boldsymbol{\mu}) \tag{2.51}\]

我们可以把 ${y_{i}}$ 表示成单位正交向量 $\boldsymbol{u}_{i}$ 关于原始的 $x_{i}$ 坐标经过平移和旋转后形成的新的坐标系。

定义向量 $\boldsymbol{y}=\left(y_{1}, \ldots, y_{D}\right)^{T}$, 我们有

\[\boldsymbol{y}=\boldsymbol{U}(\boldsymbol{x}-\boldsymbol{\mu}) \tag{2.52}\]

其中 $\boldsymbol{U}$ 是一个矩阵, 它的行是向量 $\boldsymbol{u}_{i}^{T}$ 。从公式（2.46）可以看出 $\boldsymbol{U}$ 是一个正交 orthogonal矩阵, 即它满足性质 $\boldsymbol{U} \boldsymbol{U}^{T}=\boldsymbol{I}$, 因此也满足 $\boldsymbol{U}^{T} \boldsymbol{U}=\boldsymbol{I}$, 其中 $\boldsymbol{I}$ 是单位矩阵。二次型在公式 $(2.50)$ 为常数的曲面上为常数, 因此高斯密度也是常数。

如果所有的特征值 $\lambda_{i}$ 都是正数, 那么这些曲面表示椭球面, 椭球中心位于 $\boldsymbol{\mu}$, 椭球的轴的方向沿着 $\boldsymbol{u}_{i}$, 沿着轴向的缩放因子为 $\lambda_{i}^{\frac{1}/{2}}$, 如图2.7所示。

# 图2.7 椭球面
fig, ax = plt.subplots(figsize=(5, 5))
d = plt.imread('./graph/figure2.7.png't)
plt.axis('off')
ax.imshow(d)

svg

协方差矩阵的所有特征值都严格大于零，为了正确归一化。这就是正定矩阵。(2.57解释)

如果所有特值都是非负的，就是半正定矩阵。

坐标变换

在$ y_j $坐标系下，高斯分布由以下形式：

\[p(\boldsymbol{y})=p(\boldsymbol{x})\mid \boldsymbol{J}\mid =\prod_{j=1}^{D} \frac{1}{\left(2 \pi \lambda_{j}\right)^{\frac{1}{2}}} \exp \left\{-\frac{y_{j}^{2}}{2 \lambda_{j}}\right\} \tag{2.56}\]

期望：

\[\begin{aligned} \mathbb{E}[\boldsymbol{x}] &=\frac{1}{(2 \pi)^{\frac{D}{2}}} \frac{1}{\mid \mathbf{\Sigma}\mid ^{\frac{1}{2}}} \int \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\} \boldsymbol{x} \mathrm{d} \boldsymbol{x} \\ &=\frac{1}{(2 \pi)^{\frac{D}{2}}} \frac{1}{\mid \boldsymbol{\Sigma}\mid ^{\frac{1}{2}}} \int \exp \left\{-\frac{1}{2} \boldsymbol{z}^{T} \boldsymbol{\Sigma}^{-1} \boldsymbol{z}\right\}(\boldsymbol{z}+\boldsymbol{\mu}) \mathrm{d} \boldsymbol{z} \end{aligned} \tag{2.58}\]

用$z=x-\mu$替换

\[\mathbb{E}[X] = \mu \tag{2.59}\]

二阶矩是：

\[\begin{aligned} \mathbb{E}\left[\boldsymbol{x} \boldsymbol{x}^{T}\right] &=\frac{1}{(2 \pi)^{\frac{D}{2}}} \frac{1}{\mid \mathbf{\Sigma}\mid ^{\frac{1}{2}}} \int \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\} \boldsymbol{x} \boldsymbol{x}^{T} \mathrm{d} \boldsymbol{x} \\ &=\frac{1}{(2 \pi)^{\frac{D}{2}}} \frac{1}{\mid \boldsymbol{\Sigma}\mid ^{\frac{1}{2}}} \int \exp \left\{-\frac{1}{2} \boldsymbol{z}^{T} \boldsymbol{\Sigma}^{-1} z\right\}(\boldsymbol{z}+\boldsymbol{\mu})(\boldsymbol{z}+\boldsymbol{\mu})^{T} \mathrm{d} \boldsymbol{z} \end{aligned}\]

$也用z=x-\mu$来替换。交叉项$\mu z^T和z\mu^T$因为对称性抵消，$\mu\mu^T$为常数可以拿出，本身又是单位向量被归一化。对于$zz^T$项，我们可以得到 $z = \sum\limits_{j=1}^Dy_ju_j \tag{2.60}$

其中$ y_j = u_j^Tz $

所以

\[\mathbb{E}[XX^T] = \mu\mu^T + \Sigma \tag{2.62}\]

所以

\[var[X] = \mathbb{E}[(X - \mathbb{E}[X])(X - \mathbb{E}[X])^T] \tag{2.63}\] \[var[X] = \Sigma\]

高斯分布的问题，参数太多，平方增长，无法求逆。

一个对称协方差$\Sigma$有$D(D+1)/2$个参数,$\mu$有D个参数，一共$D(D+3)/2$个参数。
一个对角协方差矩阵$\Sigma=diag(\sigma_i^2)$，一共2D个参数
再正比于单位矩阵$\Sigma=\sigma^2I$,一共D+1个参数。

另一局限性是单峰的，不能近似多峰问题，可以近似的概率有限。

引入潜在变量来解决（HMM，卡尔曼滤波器，马尔可夫随机场之类）。

2.3.1条件高斯分布

多元高斯性质：两个变量的联合高斯分布，一个变量为条件的高斯分布也是高斯分布。边缘高斯分布也是高斯分布。这节看条件高斯分布。

假设$x $是服从高斯分布$ \mathcal{N}(x\mid \mu, \Sigma) $的$D $维向量，把$ x $划分为两个不相交的子集$ x_a, x_b $。令$ x_a $为$ x $的前$ M $个分量，令$ x_b $为剩余的$ D − M $个分量，得到：

\[\boldsymbol{x}=\left(\begin{array}{l} \boldsymbol{x}_{a} \\ \boldsymbol{x}_{b} \end{array}\right) \tag{2.65}\] \[\boldsymbol{\mu}=\left(\begin{array}{l} \boldsymbol{\mu}_{a} \\ \boldsymbol{\mu}_{b} \end{array}\right) \tag{2.66}\] \[\boldsymbol{\Sigma}=\left(\begin{array}{cc} \boldsymbol{\Sigma}_{a a} & \boldsymbol{\Sigma}_{a b} \\ \boldsymbol{\Sigma}_{b a} & \boldsymbol{\Sigma}_{b b} \end{array}\right) \tag{2.67}\]

协方差矩阵是对称的即$ \Sigma^T = \Sigma $，可得$\Sigma_{aa},\Sigma_{bb} $也是对称的，且$ \Sigma_{ba} = \Sigma_{ab}^T $。

在很多情况下，使用协方差的逆矩阵会比较方便，记：

\[\Lambda \equiv \Sigma^{-1} \tag{2.68}\]

这被称为精度矩阵（precision matrix）。

\[\boldsymbol{\Lambda}=\left(\begin{array}{cc} \boldsymbol{\Lambda}_{a a} & \boldsymbol{\Lambda}_{a b} \\ \boldsymbol{\Lambda}_{b a} & \boldsymbol{\Lambda}_{b b} \end{array}\right) \tag{2.69}\]

因为对称矩阵的逆同样是对称的，所以$ \Lambda_{aa},\Lambda_{bb} $也是对称的，且$ \Lambda_{ab}^T = \Lambda_{ba} $。

需要强调的一点是：$ \Lambda_{aa} $不单单是对$ \Sigma_{aa} $求逆这么简单。

首先，找到条件分布$ p(x_a\mid x_b) $的条件分布。

根据概率的乘法规则，由联合分布 $ p(x) = p(x_a, x_b) $通过固定$ x_b $为观测到的值，然后标准化所得到的表达式就可以得到$ x_a $上的有效概率。（为什么？）

简单说就是先算二次型，再算系数。确定均值和方差。

二次型：

\[-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu) = \ -\frac{1}{2}(x_a - \mu_a)^T\Lambda_{aa}(x_a - \mu_a) -\frac{1}{2}(x_a - \mu_a)^T\Lambda_{ab}(x_b - \mu_b) \\ -\frac{1}{2}(x_b - \mu_b)^T\Lambda_{ba}(x_a - \mu_a) -\frac{1}{2}(x_b - \mu_b)^T\Lambda_{bb}(x_b - \mu_b) \tag{2.70}\]

把它看成$ x_a $的函数，这又是一个二次型，可以推出对应的条件分布$ p(x_a\mid x_b) $是高斯分布。

一个通用的的高斯分布$ \mathcal{N}(x\mid \mu, \Sigma) $的指数项可以写成：

\[-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu) = -\frac{1}{2}x^T\Sigma^{-1}x + x^T\Sigma^{-1}\mu + const \tag{2.71}\]

“完成平⽅项”：直接对应系数就可以求得均值和方差。

如果我们选出所有$x_a $的二阶项，就有：

\[-\frac{1}{2}x_a^T\Lambda_{aa}x_a \tag{2.72}\]

从这个公式中可以得到，$ p(x_a\mid x_b) $的协方差（精度矩阵的逆）：

\[\Sigma_{a\mid b} = \Lambda_{aa}^{-1} \tag{2.73}\]

现在，考虑式（2.70）中$ x_a $的所有线性项：

\[\boldsymbol{x}_{a}^{T}\left\{\boldsymbol{\Lambda}_{a a} \boldsymbol{\mu}_{a}-\boldsymbol{\Lambda}_{a b}\left(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b}\right)\right\} \tag{2.74}\]

所以， $\begin{aligned} \boldsymbol{\mu}_{a \mid b} &=\boldsymbol{\Sigma}_{a \mid b}\left\{\boldsymbol{\Lambda}_{a a} \boldsymbol{\mu}_{a}-\boldsymbol{\Lambda}_{a b}\left(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b}\right)\right\} \\ &=\boldsymbol{\mu}_{a}-\boldsymbol{\Lambda}_{a a}^{-1} \boldsymbol{\Lambda}_{a b}\left(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b}\right) \end{aligned} \tag{2.75}$

根据分块矩阵的逆矩阵的恒等式，换用分块协⽅差矩阵来表示，条件概率$ p(x_a\mid x_b) $的均值和方差

\[\boldsymbol{\mu}_{a \mid b}=\boldsymbol{\mu}_{a}+\boldsymbol{\Sigma}_{a b} \boldsymbol{\Sigma}_{b b}^{-1}\left(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b}\right) \tag{2.81}\] \[\boldsymbol{\Sigma}_{a \mid b}=\boldsymbol{\Sigma}_{a a}-\boldsymbol{\Sigma}_{a b} \boldsymbol{\Sigma}_{b b}^{-1} \boldsymbol{\Sigma}_{b a} \tag{2.82}\]

均值是$x_b$的线性函数。

2.3.2 边缘⾼斯分布

分区高斯的边缘或条件分布总结如下：

对于联合高斯分布$\mathcal{N}(x\mid \mu,\Sigma) , \Lambda \equiv \Sigma^{-1}$如果拆成两块。

\[\begin{aligned} \boldsymbol{x} &=\left(\begin{array}{c} \boldsymbol{x}_{a} \\ \boldsymbol{x}_{b} \end{array}\right), \quad \boldsymbol{\mu}=\left(\begin{array}{c} \boldsymbol{\mu}_{a} \\\boldsymbol{\mu}_{b} \end{array}\right) \\ \boldsymbol{\Sigma}&=\left(\begin{array}{cc} \mathbf{\Sigma}_{a a} & \boldsymbol{\Sigma}_{a b} \\ \boldsymbol{\Sigma}_{b a} & \boldsymbol{\Sigma}_{b b} \end{array}\right), \quad \boldsymbol{\Lambda}=\left(\begin{array}{cc} \boldsymbol{\Lambda}_{a a} & \boldsymbol{\Lambda}_{a b} \\ \boldsymbol{\Lambda}_{b a} & \boldsymbol{\Lambda}_{b b} \end{array}\right) \end{aligned} \tag{2.94,2.95}\]

条件分布：

\[p(x_a\mid x_b) = \mathcal{N}(x\mid \mu_{a\mid b}, \Lambda_{aa}^{-1}) \tag{2.96}\] \[\mu_{a\mid b} = \mu_a - \Lambda_{aa}^{-1}\Lambda_{ab}(x_a - \mu_b) \tag{2.97}\]

边缘分布：

\[p(x_a) = \mathcal{N}(x_a\mid \mu_a, \Sigma_{aa}) \tag{2.98}\]

# 图2.9展示涉及到两个变量的多元高斯分布的条件概率分布和边缘概率分布
fig, (ax1,ax2) = plt.subplots(1,2,figsize=(10, 5),dpi=300)
d1 = plt.imread('./graph/Figure2.9a.png')
d2 = plt.imread('./graph/Figure2.9b.png')
ax1.imshow(d1)
ax2.imshow(d2)
ax1.axis('off')
ax2.axis('off')

(-0.5, 1666.5, 1657.5, -0.5)

svg

2.3.3 ⾼斯变量的贝叶斯定理

假设给定高斯边缘分布$ p(x) $和均值是关于$ x $的线性函数且方差与$ x $无关的高斯条件分布$ p(y\mid x) $。这是线性高斯模型（linear Gaussian model）的一个例子。

把边缘和条件分布记为：

\[\begin{array}{r} p(\boldsymbol{x})=\mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Lambda}^{-1}\right) \\ p(\boldsymbol{y} \mid \boldsymbol{x})=\mathcal{N}\left(\boldsymbol{y} \mid \boldsymbol{A} \boldsymbol{x}+\boldsymbol{b}, \boldsymbol{L}^{-1}\right) \end{array} \tag{2.99,2.100}\]

其中$ \mu, A, b $是控制均值的参数，$ \Lambda , L $是精度矩阵。设$ x,y $分别是$ M,D $维的，那么矩阵$ A $是$ D \times M $矩阵。

首先求x，y的联合分布。

\[z = \left( \begin{array}{c} x \\ y \end{array} \right) \tag{2.101}\]

求对数：

\[\begin{split} \ln p(z) &= \ln p(x) + \ln p(y\mid x) \\ &= -\frac{1}{2}(x - \mu)^T\Lambda(x-\mu) \\ &-\frac{1}{2}(y-Ax-b)^TL(y-Ax-b) + const \end{split} \tag{2.102}\]

常数是与x，y无关的项。z的分量的二次函数》高斯函数。

为了计算高斯分布的精度，看二阶项：

\[-\frac{1}{2} \boldsymbol{x}^{T}\left(\boldsymbol{\Lambda}+\boldsymbol{A}^{T} \boldsymbol{L} \boldsymbol{A}\right) \boldsymbol{x}-\frac{1}{2} \boldsymbol{y}^{T} \boldsymbol{L} \boldsymbol{y}+\frac{1}{2} \boldsymbol{y}^{T} \boldsymbol{L} \boldsymbol{A} \boldsymbol{x}+\frac{1}{2} \boldsymbol{x}^{T} \boldsymbol{A}^{T} \boldsymbol{L} \boldsymbol{y}\] \[=-\frac{1}{2}\left(\begin{array}{c} \boldsymbol{x} \\ \boldsymbol{y} \end{array}\right)^{T}\left(\begin{array}{cc} \boldsymbol{\Lambda}+\boldsymbol{A}^{T} \boldsymbol{L} \boldsymbol{A} & -\boldsymbol{A}^{T} \boldsymbol{L} \\ -\boldsymbol{L} \boldsymbol{A} & \boldsymbol{L} \end{array}\right)\left(\begin{array}{l} \boldsymbol{x} \\ \boldsymbol{y} \end{array}\right)=-\frac{1}{2} \boldsymbol{z}^{T} \boldsymbol{R} \boldsymbol{z} \tag{2.103}\]

R就是精度矩阵。用2.76求逆得到协方差矩阵：

\[cov[z] = R^{-1} = \left( \begin{array}{cc} \Lambda^{-1} & \Lambda^{-1}A^T \\ A\Lambda^{-1} & L^{-1} + A\Lambda^{-1}A^T \end{array} \right) \tag{2.105}\]

用2.102的一阶项计算z的均值。先找到一阶项：

\[x^T\Lambda\mu - x^TA^TLb + y^TLb = \left( \begin{array}{c} x \\ y \end{array} \right)^T \left( \begin{array}{c} \Lambda\mu - A^TLb \\ Lb \end{array} \right) \tag{2.106}\]

跟2.71对比求出均值表达式。

$\mathbb{E}[z] = R^{-1} \left( \begin{array}{c} \Lambda\mu - A^TLb \\ Lb \end{array} \right) \tag{2.107}$ 用2.106带入计算结果

\[\mathbb{E}[z] = \left( \begin{array}{c} \mu \\ A\mu + b \end{array} \right) \tag{2.108}\]

计算边缘分布y的表达式.直接利用2.92和2.93就可得到结果：

\[\begin{split} \mathbb{E}[y] = A\mu + b \end{split} \tag{2.109}\] \[cov[y] = L^{-1} + A\Lambda^{-1}A^T \tag{2.110}\]

当A=I，均值就是两个之和（是均值为$\mu和b$的两个高斯分布之和），方差也是两个之和。

最后，求$ p(x\mid y) $。用2.73和2.75来对比2.105和2.108.得到方差和均值：

\[\begin{aligned} \mathbb{E}[\boldsymbol{x} \mid \boldsymbol{y}]=&\left(\boldsymbol{\Lambda}+\boldsymbol{A}^{T} \boldsymbol{L} \boldsymbol{A}\right)^{-1}\left\{\boldsymbol{A}^{T} \boldsymbol{L}(\boldsymbol{y}-\boldsymbol{b})+\boldsymbol{\Lambda} \boldsymbol{\mu}\right\} \\ & \operatorname{cov}[\boldsymbol{x} \mid \boldsymbol{y}]=\left(\boldsymbol{\Lambda}+\boldsymbol{A}^{T} \boldsymbol{L} \boldsymbol{A}\right)^{-1} \end{aligned} \tag{2.111,2.112}\]

总结：

对于$ x $的边缘高斯分布和$ y $关于$ x $的条件高斯分布：

\[p(x) = \mathcal{N}(x\mid \mu,\Lambda^{-1}) \tag{2.113}\] \[p(y\mid x) = \mathcal{N}(y\mid Ax + b,L^{-1}) \tag{2.114}\]

那么$ y $的边缘分布和$ x $关于$ y $的条件高斯分布为：

\[p(y) = \mathcal{N}(y\mid A\mu + b,L^{-1} + A\Lambda^{-1}A^T) \tag{2.115}\] \[p(x\mid y) = \mathcal{N}(x\mid \Sigma\left\{A^TL(y-b) + \Lambda\mu \right\},\Sigma) \tag{2.116}\]

其中

\[\Sigma = (\Lambda + A^TLA)^{-1} \tag{2.117}\]

上篇PRML笔记 Ch1.绪论

下篇深度学习在检测音乐节拍Onset中的应用