摘要
本文探讨了深度学习在音乐节拍跟踪方向的应用,举例说明了几类常见的神经网络算法。另外,本文对文献[1]所用的RNN网络模型进行了探究试验,在自建数据集上进行训练和测试,并与通用信号处理框架进行比较,结果表明RNN在F-measure和P-score两项精度指标上均占优,但仍存在模型不稳定的问题。
1. 引言
节拍(Beat)是指某种具有固定时长的音符,通常以四分音符或八分音符为一拍。节拍跟踪/节拍检测是计算机对人们在听音乐时无意识踮脚或拍手对现象的模拟,经常用于对音乐信号按节拍进行分割[2]。节拍是理解音乐节奏的基础,在视频编辑、音乐可视化、舞台灯光控制等方面有许多应用。
大多数早期的节拍跟踪的研究使用符号音乐或乐器数字接口(Musical Instrument Digital Interface, MIDI)数据,而且大多不能实时工作。后来开始出现可以处理音乐声音信号来处理的算法。例如Brown[3]使用自相关运算检验信号中的脉冲是否为拍子。Scheirer[4]提出的共振器模型预先对信号进行分频,然后计算每个子带的幅度包络和导数,再与一组梳状滤波器进行卷积,对所有子带上的能量求和后得到一系列峰值。Goto[5]等人的多代理模型针对音乐中没有打击乐器或不明显的情况提出采用和弦改变点作为节拍候选点。传统的节拍检测方法通常只处理音频信号的频谱或相位信息,信号变换的手段包括短时傅里叶变换、小波变换、常数Q变换、稀疏分解等,Bello[6]对这类方法做了很好的概述。
近年来,基于机器学习的节拍或起始点检测算法取得了很大的成功。特别是,深度神经网络的引入极大地提高了节拍跟踪系统的准确性[7–9],依赖深度学习的系统已成为目前最先进的技术。
2. 深度学习在节拍跟踪的应用
早在2005年,Lacoste[10]等人就将MLP应用于节拍跟踪,对每一帧二分类为节拍和非节拍帧。基于卷积神经网络的算法用卷积神经网络来学习音符起始点的特征,常用的卷积神经网络模型包括CNN、TCN等。基于循环神经网络的算法通过传递隐含变量,学习音符起始点的时序信息,常用模型包括RNN、LSTM、BLSTM等。基于卷积循环神经网络的算法结合了卷积神经网络和循环神经网络的优点,使用卷积神经网络来学习音符起始点的局部特征,使用循环神经网络来学习音符起始点的时序信息,并对输入音频流进行实时检测,常用的模型包括CRNN等。最近,基于注意力机制的模型Transformer、Attention-RNN在计算机视觉和自然语言处理方向上得到了广泛的应用。与RNN一样,Transformer用于处理顺序数据,包括不同尺度的上下文信息,与RNN不同的是,Transformer是可以大规模并行计算的,因为它是前馈网络。下面列举节拍跟踪应用中几种常见机器学习算法。
2.1 FNN
前馈神经网络(Feedforward neural networks, FNN),或多层感知器(Multi-layer perceptron,MLP),是典型的深度学习模型。MLP是最简单的人工神经网络类型[11]。在这个网络中,信息只向一个方向移动,从输入节点向前移动到输出节点。因此,网络中没有循环。Lacoste[10]等人使用经典的预测框架将预测步骤分为3步:
- 第1步将声音通过短时傅里叶变换得到频谱特征序列;
- 第2步,将特征输入神经网络得到节拍或音符起始点可能性的概率曲线;
- 第3步通过某些峰值提取的方法得到最终预测的节拍序列。
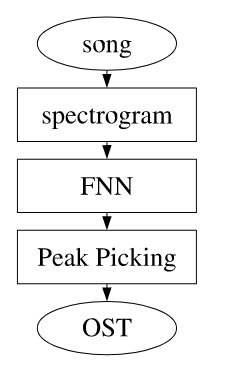
图片:FNN神经网络经典预测框架
2.2 CNN
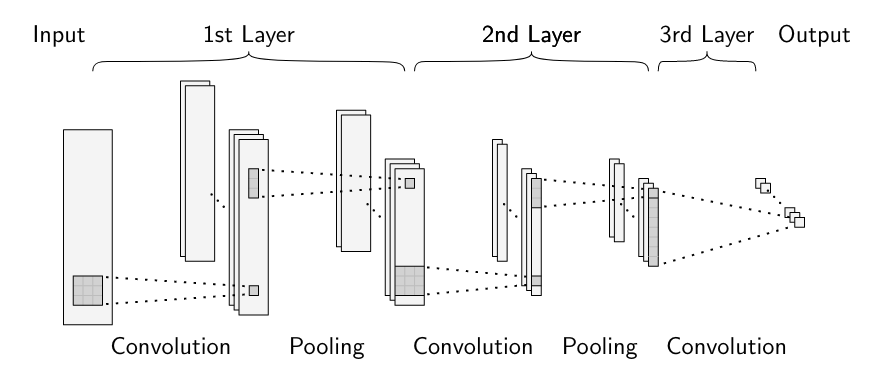
卷积神经网络(Convolutional Neural Networks,CNN)[12]是一类深度神经网络,专门用于处理具有类似网格拓扑的数据,一维时间序列或二维图像数据。CNN是前馈神经网络的正则化版本,只需在其至少一个层中使用卷积来代替一般矩阵乘法。通常,卷积神经网络中使用的操作并不完全对应于卷积的数学定义。相反,许多神经网络模型使用的是交叉相关。
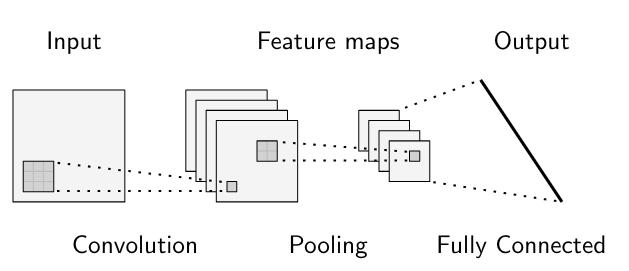
图片:典型卷积神经网络结构
文献[13]探讨了一种用于检测起始点的CNN网络模型,其性能与RNN相当, CNN虽然计算成本更高,但在网络训练上更有优势,RNN需要迭代计算,而CNN可以使用GPU加速并行计算。
![文献[13] 采用的CNN网络结构](/pictures/DLOnsetDet/image005.png)
图片:文献[13] 采用的CNN网络结构
2.3 RNN
循环神经网络(Recurrent Neural Network,RNN)通过使用带自反馈的神经元,能够处理任意长度的时序数据。一个完全连接的循环网络是任何非线性动力系统的近似器。在节拍跟踪任务中主要工作在同步的序列到序列模式,通过不断输入特征帧向量获得当前帧为节拍的概率输出。由于RNN的计算量很小,而且算法时因果的,因此其十分适合于实时节拍检测。循环神经网络的参数包括隐藏层的权重 和偏置 ,以及输出层的权重 和偏置 ,实现小而简洁的网络模型,便于提高推理速度。
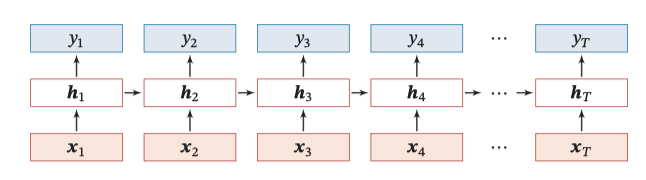
图片:循环神经网络的结构及推理顺序示意
如果使用两个独立的隐藏层,都连接到相同的输入和输出层。第一个隐藏层向前处理输入序列,第二个隐藏层向后处理输入序列。这样得到网络始终可以对称地访问完整的过去和未来的信息,这成为双向循环网络(Bidirectional Recurrent Neural Networks,BRNN)。BRNN的缺点是必须有完整的输入序列才能进行处理。文献[1]通过RNN实现了一个实时的起始点检测系统,其检测速度高于人类感知的速度。
![文献[1]提出的RNN网络音符起始点检测系统](/pictures/DLOnsetDet/image017.png)
图片:文献[1]提出的RNN网络音符起始点检测系统
2.4 CRNN
卷积循环神经网络(Convolutional Recurrent Neural Networks,CRNN)结合了CNN和RNN的特点,将循环层连接到卷积模型的输出[14,15]。CRNN与RNN和CNN的区别在于,RNN按顺序处理输入,在训练时通常只使用输入信号的子序列来减少网络的内存占用。CNN通常也是逐帧处理信号,但不能感知整个序列。CRNN和RNN一样,按顺序处理输入,但除此之外还会进行对频谱进行卷积来感知上下文。
![在频谱图上比较RNN、CNN和CRNN的运行模式[14]](/pictures/DLOnsetDet/image019.png)
图片:在频谱图上比较 RNN、CNN 和 CRNN 的运行模式[14]
2.5 LSTM
虽然BRNN可以访问过去和未来的信息,但由于消失的梯度问题,感受范围仅限于几帧。输入值的影响随着时间的推移呈指数级下降或膨胀,并由新的输入值主导。为了克服这一缺陷,文献[16]引入了一种称为长期短期记忆(Long Short Term Memory,LSTM)的方法。在LSTM隐藏层中,非线性单元被LSTM内存块取代。
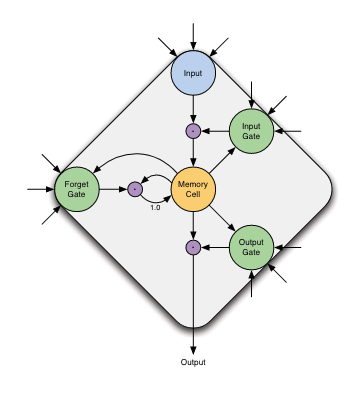
图片:带有一个内存单元的LSTM块
2.6 TCN
时间卷积网络(Temporal Convolutional Network, TCN)[17]首次出现在著名的原始音频信号生成模型WaveNet[18]模型中,它使用扩张卷积(即跨子采样输入表示的卷积)以学习顺序/时序结构。简单卷积的缺点是只以网络深度大小访问序列。TCN采用了扩展的卷积,得到指数级放大的感受野,延伸数百帧的上下文。Matthew[8]等人使用TCN做时间维度上的扩张卷积,学习了16维特征向量,以预测音乐节拍的位置。此外,TCN具有的高度并行性,因此可以在GPU上非常高效地进行训练,速度是BLSTM的60倍[8]。

图片:TCN节拍检测系统
1)输入特征表示:计算对数幅值谱,步长10ms,窗宽46.4ms。映射到每八度12频段的对数滤波器组,得到总共81个频段输入特征,覆盖30 Hz到17 kHz。 2)卷积块:3个卷积层:前2层有16个尺寸为3×3的滤波器,在频率方向上进行宽度为3的Max pooling;第三层有16个尺寸为1×8的滤波器,不进行pooling。激活函数采用指数线性单位(ELU),随后Dropout,丢弃率为0.1。通过频谱卷积,每5帧频谱片段(包含重叠)被压缩为1帧,总计16个特征。
图片:卷积块结构
3)时域卷积网络:具有11个堆叠残差块,每个块具有两层膨胀卷积组成,滤波器大小k = 5。膨胀系数d = 2i随着添加堆栈级别i而几何变宽。
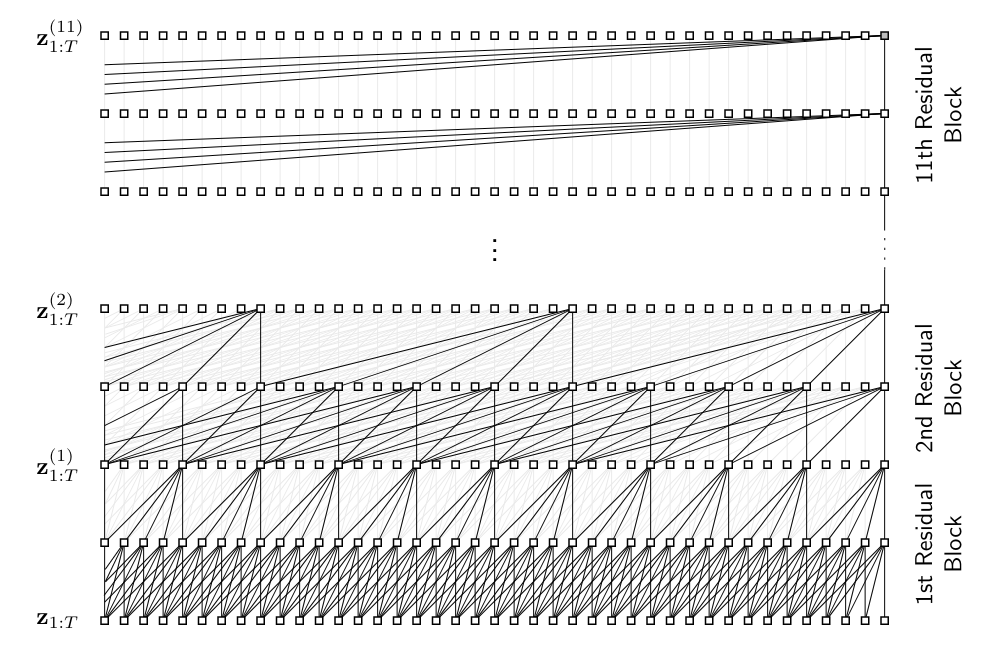
图片:TCN结构
3. 实验探究
本文对文献[1]所用的RNN网络模型进行了探究试验,在自建数据集上进行训练和测试,并与通用信号处理方法进行了对比。
3.1 输入特征处理
对于采样率44.1kHz的音频,步长10ms,窗宽11.6ms,23.2ms和46.4ms( W=521,1024 和 2048),得到频谱 $X(n,k)$ ,然后转换为能量谱,然后经40通道三角滤波器组将能量谱$S(n,k)$转换为Mel谱$M(n,M)$ ,并做对数变换以匹配人类听觉响度曲线
\[M_{\log}= \log(M(n,M)+1.0)\]3.2 RNN网络
- 输入层:分别计算窗宽为11.6ms,23.2ms和46.4ms,Mel通道数80的Mel谱 \(M^{12}_{\log}\) ,\(M^{23}_{\log}\) 和 ,\(M^{46}_{\log}\) 总计240个输入单元。
- 隐藏层:由d=3个全连接循环隐藏层组成,每个层有h=20个带有tanh的标准神经元。
- 输出层:2个神经元,使用softmax函数归一化。
3.3 数据集准备
本文采用的数据集是自建数据集Spotify Dance Pop Hits,包含114曲英文舞曲流行音乐,标准化为WAVE格式音频,截取持续时间不超过3min的部分作为训练音频。这些音乐具有较强的鼓点,在音符起始点的位置上往往有较强的能量尖峰。所有数据集114曲中,随机划分出89曲作为训练集,14曲作为验证集,剩余11曲作为测试数据。
由于音符起始点的人工标注难度很高,并且,数据集规模较大,本文实验采取的起始点标签真值通过一款开源软件Madmom[19]中基于多模型动态贝叶斯网络的方法提取,为了剔除干扰,合并检测到的间隔小于200ms的起始点。图5展示了部分训练数据的情况,(a)是原始音频波形,(b)是经过短时傅里叶变换得到的时频谱图输入数据,白色标注是数据的起始点真值标签。
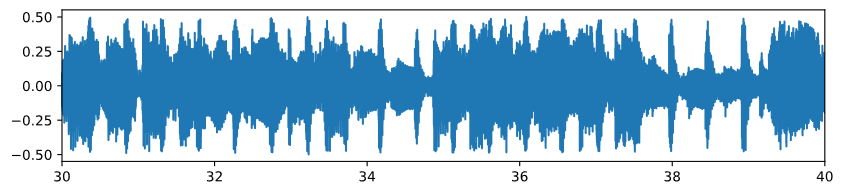
( a ) 音频波形
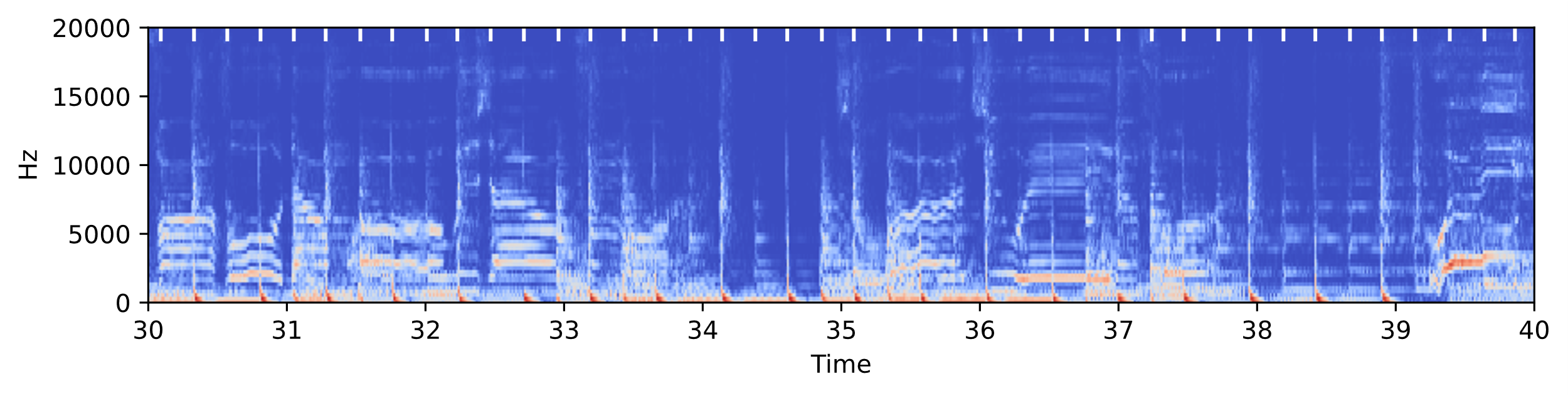
( b ) Mel谱图,白色标注帧为起始点标签
图片:you broke me first - Gryffin Remix 波形和 Mel谱(部分)
3.4 精度评价指标
起始点检测的精度指标采用F-measure和P-Score两个指标进行定量评估,这两个指标平衡了精确度和错误率,综合评价了模型算法的对于起始点的检测精度。
F-measure的计算方法是将标注值的一个25ms的邻域内的待测值标记为正确,然后计算召回率recall和精确率precision,F-measure为
\[F = \frac{2}{\text{Recall}^{-1}+\text{Precision}^{-1}}\]P-score计算方法对待测脉冲序列和标注脉冲序列做互相关运算,脉冲序列由所有节拍位置上幅值为1的单位脉冲叠加构成。当待测值落入标注值一个宽度20%起始点间隔的邻域时,则认为待测值正确。
\[P= \frac{N_{\text{correct}}}{N_{\max}}\]$N_{\max}$是待测起始点个数与标注起始点个数两者之中的较大者。
3.5 模型训练
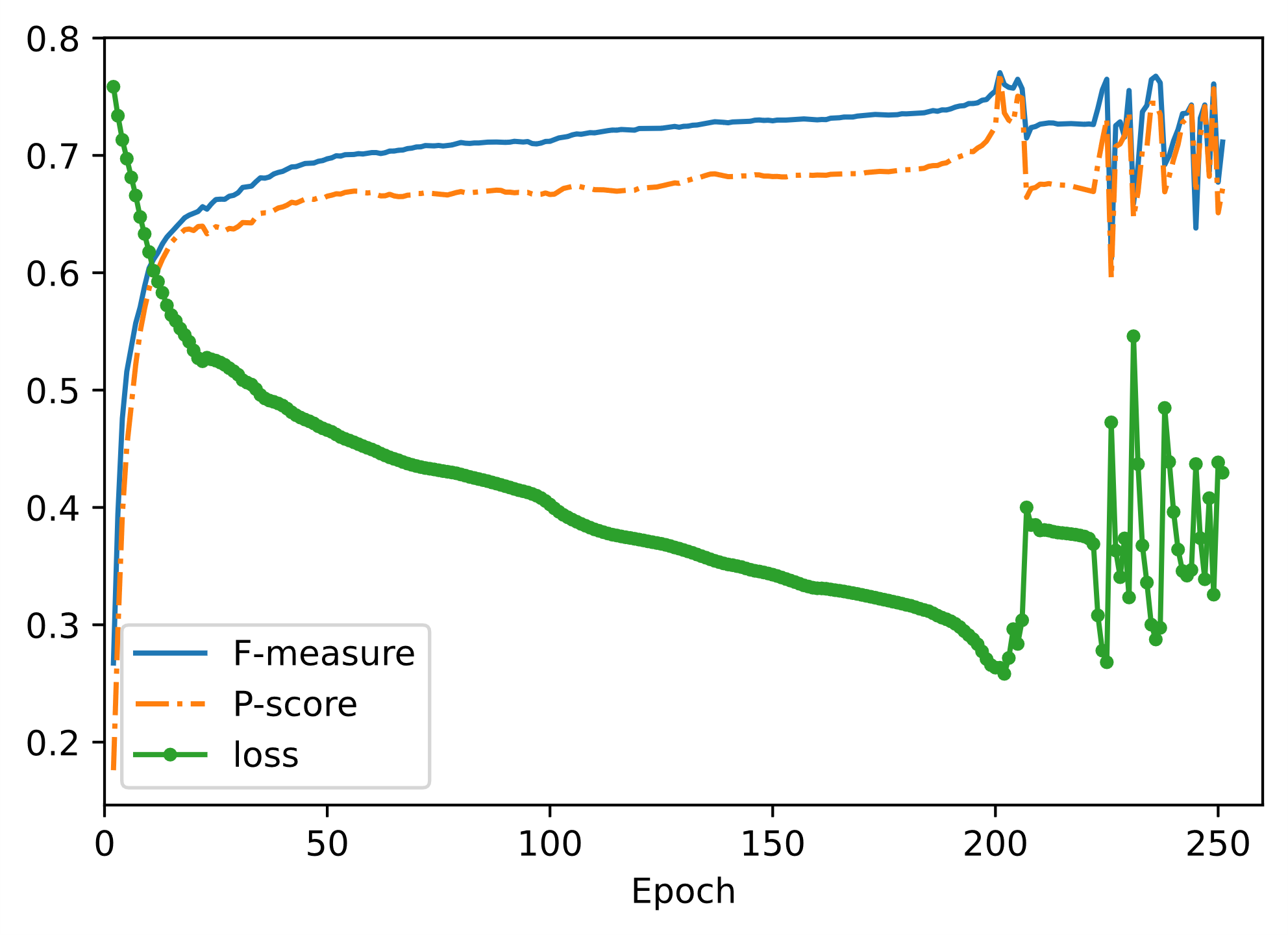
由于超参数较多,受制于算力条件,首先进行几次预训练,发现将学习率定为0.1,批大小为4096较为合适。之后,进行250轮训练,得到了损失函数和精度指标随着训练轮数变化的曲线如图6,可以发现在大约200轮训练之后损失函数降低到最小,精度指标得到最高,表明模型已经收敛;200轮之后,损失函数和精度指标开始剧烈振荡,表明模型可能出现了梯度爆炸的现象。因此,正式训练时选定训练轮数为200,得到了最终的模型。该模型用于最后评估精度,且会把LibROSA[20]的检测精度作为基准进行比较。
图片:训练损失和验证精度
3.6 结果讨论
对于同一段测试音频,RNN神经网络输出和LibROSA的输出如图所示。其中上半子图是音频的频谱,下半子图的实曲线表示起始点的概率/强度,虚线标记的帧是峰值提取得到的起始点位置,黑色和白色标记帧是真值标签。可以直观看到,对比LibROSA输出的起始点强度曲线,RNN网络输出的结果有着更好的稀疏性,在起始点位置有更强的概率峰值,很好的剔除了非起始点帧的噪声干扰,而且峰值的均匀度更好,经峰值提取之后具有更优的精度。
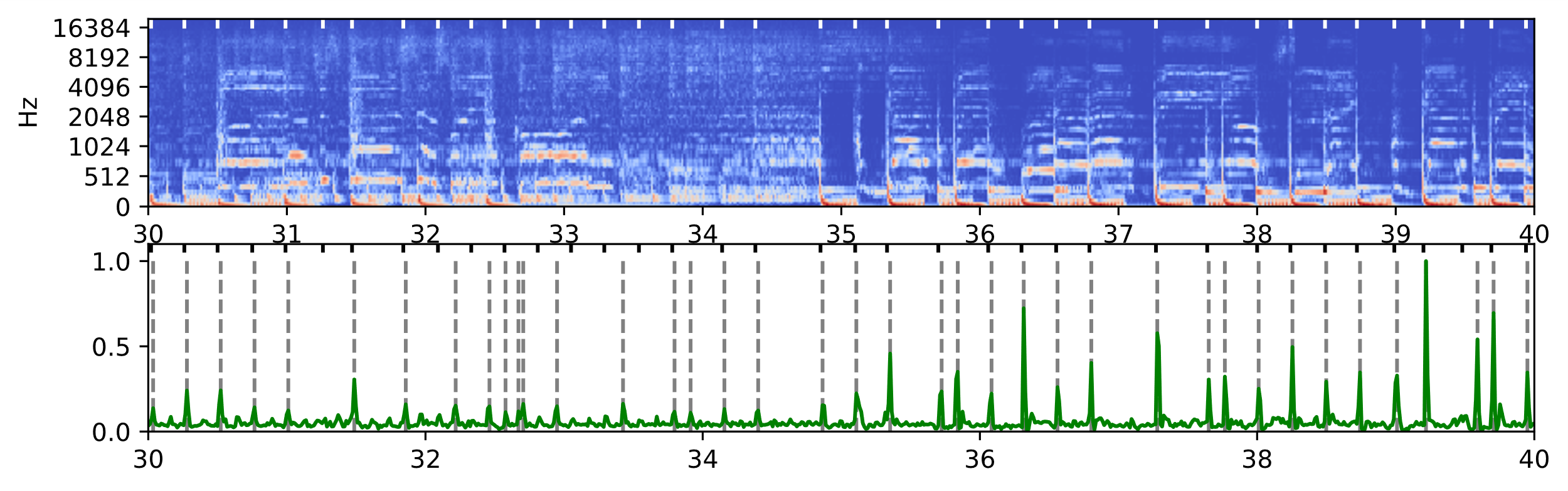
(a) LibROSA
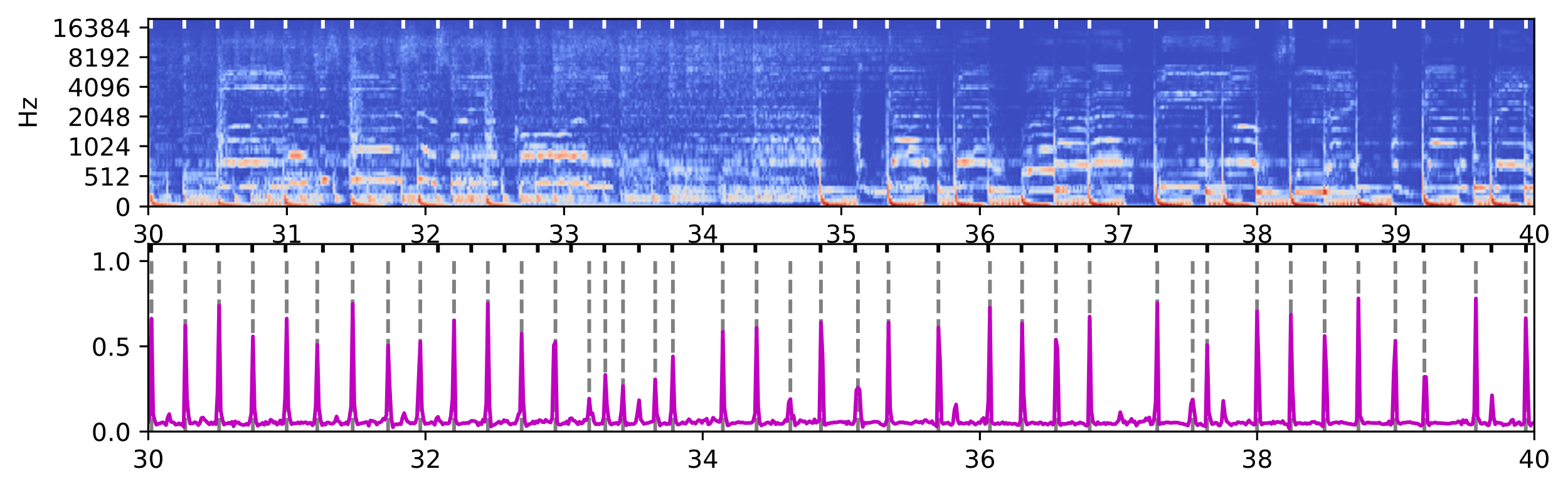
(b) RNN
图片:LibROSA的输出和RNN神经网络输出
RNN和LibROSA输出结果对比,灰色虚线是提取的峰值点,黑色标记点是标注真值(测试数据:test/01 BED.wav 30s-40s)
对于两种算法的精度评估的结果如表所示。评估实验结果表明,相比于LibROSA,RNN网络的召回率Recall略低于LibROSA,但是在精确率Precision上大幅优于LibROSA,因此,在F-measure和P-score两项精度指标上均优于LibROSA。
表格:精度评估结果
| Model | Recall | Precision | F-measure | P-Score |
|---|---|---|---|---|
| LibROSA[20] | 0.862 | 0.636 | 0.732 | 0.680 |
| RNN | 0.798 | 0.866 | 0.830 | 0.810 |
3.7 算法开销
本文所述算法使用PyTorch部署,能够音频流实时起始点检测任务。系统逐帧处理输入音频,步长为11.6ms,对于每个音频帧,预处理、神经网络推理和后处理花费固定的时长,并且在一台4核8线程,频率3.6 GHz的英特尔CPU的1个线程上轻松实现实时跟踪,并在PyQt上显示推理结果如图所示。
图片:实时推理示例
3.8 实验结论
基于RNN的起始点网络在音符起始点检测任务中的表现优于通用信号处理方法,网络输出的输出值对比MFCC法得到的起始点强度曲线具有更好的稀疏性和均一性,方便后续提取峰值。同时,相比LSTM网络,计算量更小,具有因果性,速度非常快。但是长时间训练后出现梯度爆炸问题导致模型不稳定,需要采取早停止等正则方法。而实际部署表明,该算法能够在普通PC上完成实时计算。需要注意的是,本次实验没有在更复杂的数据集上进行评估,对于流行题材以外的音乐,以及实际应用场景下的有如录音混响、环境噪声、压缩重采样等各种音质损失时,可能需要更新对应的数据集,算法的表现需要重新验证。
参考文献
[1] Böck, Sebastian, et al. Online real-time onset detection with recurrent neural networks[J].Proceedings of the 15th International Conference on Digital Audio Effects (DAFx-12), York, UK. sn, 2012.
[2] 李伟, 李子晋, 高永伟. 理解数字音乐——音乐信息检索技术综述[J].复旦学报: 自然科学版 57.3 (2018): 271-313.
[3] Brown, Judith C. Determination of the meter of musical scores by autocorrelation[J]. The Journal of the Acoustical Society of America 94.4 (1993): 1953-1957.
[4] Scheirer, Eric D. Tempo and beat analysis of acoustic musical signals. The Journal of the Acoustical Society of America 103.1 (1998): 588-601.
[5] Goto, Masataka. An audio-based real-time beat tracking system for music with or without drum-sounds[J]. Journal of New Music Research 30.2 (2001): 159-171.
[6] Bello, Juan Pablo, et al. A tutorial on onset detection in music signals[J]. IEEE Transactions on speech and audio processing 13.5 (2005): 1035-1047.
[7] Eyben, Florian, et al. Universal onset detection with bidirectional long-short term memory neural networks[J]. (2010).
[8] MatthewDavies, E. P., and Sebastian Böck. Temporal convolutional networks for musical audio beat tracking[C]. 2019 27th European Signal Processing Conference (EUSIPCO). IEEE, 2019.
[9] Böck, Sebastian, Matthew EP Davies. Deconstruct, Analyse, Reconstruct: How to improve Tempo, Beat, and Downbeat Estimation[J]. ISMIR. 2020.
[10] Lacoste, Alexandre, and Douglas Eck. Onset detection with artificial neural networks for mirex 2005[J]. Extended abstract of the 1st Annual Music Information Retrieval Evaluation eXchange (MIREX), held in conjunction with ISMIR (2005).
[11] Schmidhuber, Jürgen. Deep learning in neural networks: An overview[J]. Neural networks.61 (2015): 85-117.
[12] LeCun, Yann, et al. Backpropagation applied to handwritten zip code recognition[C]. Neural computation 1.4 (1989): 541-551.
[13] Schlüter, Jan, and Sebastian Böck. Improved musical onset detection with convolutional neural networks[C]. 2014 ieee international conference on acoustics, speech and signal processing (icassp). IEEE, 2014.
[14] Vogl, Richard, et al. Drum Transcription via Joint Beat and Drum Modeling Using Convolutional Recurrent Neural Networks[C]. ISMIR. 2017.
[15] Fuentes, Magdalena, et al. Analysis of common design choices in deep learning systems for downbeat tracking[C]. The 19th International Society for Music Information Retrieval Conference. 2018.
[16] Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[17] Bai S, Kolter J Z, Koltun V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling[Z]. arXiv, 2018(2018-04-19).
[18] Oord A Van Den, et al. WaveNet: A Generative Model for Raw Audio[Z]. arXiv, 2016(2016-09-19).
[19] Böck S, Korzeniowski F, Schlüter J, et al. madmom: A New Python Audio and Music Signal Processing Library[C]. Proceedings of the 24th ACM international conference on Multimedia. 2016: 1174-1178Amsterdam The Netherlands: ACM, 2016: 1174-1178.
[20] McFee, Brian, et al. librosa: Audio and music signal analysis in python[C]. Proceedings of the 14th python in science conference. Vol. 8. 2015.