卡尔曼滤波
节拍跟踪器的动力学方程描述
这里讨论在一段较短的时间内,假设音乐中节拍进行的速度是恒定的。设 $t$ 是节拍时刻,$\Delta$ 是节拍周期。已知 $k-1$ 步的节拍时刻和周期,如果不考虑噪声,在 $k$ 时刻有
节拍时间
\[\hat{t}(k)= t(k-1)+\Delta(k-1)\]节拍周期
\[\hat{\Delta}(k)= \Delta(k-1)\]于是,可以取 2 维状态向量
\[\mathrm{x} = \begin{bmatrix} t\\\Delta \end{bmatrix}\]在此基础上考虑过程噪声 $\mathrm{v}$,得到状态方程
\[\mathrm{x}(k)= \mathrm{F}\mathrm{x}(k-1)+\mathrm{v},\quad \mathrm{F}=\begin{bmatrix} 1&1\\0&1\end{bmatrix},\quad k=1,2,3, \ldots\]如果考虑观测噪声 $\mathrm{w}$,假设对节拍时刻 $t$ 进行观测,得到 1 维的观测值 $\mathrm{y}(k)=t(k)+\mathrm{w}$,得到观测方程
\[\mathrm{y}(k)=\mathrm{H}\mathrm{x}(k)+\mathrm{w},\quad \mathrm{H}=\begin{bmatrix} 1&0\end{bmatrix} ,\quad k=1,2,3, \ldots\]在这里,我们假设噪声是高斯的,且其分布不随时间变化。过程噪声 $\mathrm{v}$ 服从均值为零,协方差为 $\mathrm{Q}$ 的高斯分布。测量噪声 $\mathrm{w}$ 服从均值为零,方差为 $\mathrm{R}$ 的高斯分布。
最优估计
预测步:先验状态估计、先验估计协方差、先验观测
\[\hat{\mathrm{x}}(k) = \mathrm{F}{\mathrm{x}}(k-1)\] \[\hat{\mathrm{P}}(k) = \mathrm{F}\mathrm{P}(k-1)\mathrm{F}^{\mathrm{T}}+\mathrm{Q}\] \[\hat{\mathrm{y}}(k) = \mathrm{H}\hat{\mathrm{x}}(k-1)\]更新步:计算卡尔曼增益、后验状态估计及对应协方差
\[\mathrm{S}(k)= \mathrm{H}\mathrm{P}(k)\mathrm{H}^{\mathrm{T}}+\mathrm{R}\] \[\mathrm{K}(k)= \hat{\mathrm{P}}(k)\mathrm{H}^{\mathrm{T}}\mathrm{S}(k)^{-1}\] \[\mathrm{x}(k)=\hat{\mathrm{x}}(k) + \mathrm{K}(k)[\mathrm{y}(k)-\hat{\mathrm{y}}({k})]\] \[\mathrm{P}(k) =\left[\mathrm{I}-\mathrm{K}(k)\mathrm{H}\right]\hat{\mathrm{P}}(k)\]扩展
A. T. Cemgil, H. Kappen, P. Desain, and H. Honing. On tempo tracking: Tempogram Representation and Kalman filtering. Journal of New Music Research, 28:4:259–273, 2001.
节拍跟踪器的动力学基本模型可以在几个方向上扩展:
A.放松卡尔曼滤波器的线性约束。在一个由 $w = \log_2 \Delta$ 映射的对数空间中定义状态方程。对数映射使得周期 $\hat{\Delta}$ 永远是正的。对数映射也使得音乐速度的变化在听觉上更佳合理,例如 $\Delta \rightarrow 2\Delta$ 和 $\Delta \rightarrow \Delta/2$ 会产生相同的变化。于是
\[\hat{\tau}_j = \hat{\tau}_{j-1} + 2^{\hat{w}_{j-1}}\]B.引入惯性状态变量 $\hat{a}_j$。将状态变量 $\hat{\mathrm{x}}_j $ 扩展为 $\begin{bmatrix} \hat{\mathrm{x}}_j & \hat{a}_j \end{bmatrix}^T$。附加变量存储关于过去状态的信息,例如加速度。给系统引入惯性。惯性减少了状态空间中的随机行走行为,并使平滑的状态轨迹更有可能,并可以产生更准确的预测。
C.混合高斯建模的噪声。观测值中的离群值(Outliers)可以通过使用高斯混合来建模。例如,一个“窄”高斯用于建模正常观测,一个为“宽”高斯用于建模离群值。离散变量 $c_j$ 用于指示第 $j$ 个观测是否为离群值。这样,离群值噪声的分布为
\[\mathrm{w}_j\mid c_j \sim \mathcal{N}(0,\mathrm{R_c})\]由于 $c_j$ 不能被观测,定义先验 $c_j \sim p(c)$,然后对 $c_j$ 进行积分,即
\[\displaystyle p(\mathrm{w}_j) = \sum_{c_j}p(c_j)p(\mathrm{w}_j\mid c_j)\]于是,动力学模型变为:
\[\begin{bmatrix} \hat{\mathrm{x}}_j \\ \hat{a}_j \end{bmatrix} = \mathrm{F} \begin{bmatrix} \hat{\mathrm{x}}_{j-1} \\ \hat{a}_{j-1} \end{bmatrix}+\mathrm{v}_j\] \[\begin{bmatrix} \tau_{j} \\ w_{j} \end{bmatrix} = \begin{bmatrix} \hat{\tau}_{j} \\ \hat{w}_{j} \end{bmatrix} + \mathrm{w}_j\]其中,$c_j$ 选取为离散的开关变量,\(\mathrm{v}_j \sim \mathcal{N}(0,\mathrm{Q})\),\(\mathrm{w}_j\mid c_j \sim \mathcal{N}(0,\mathrm{R_c})\),且 \(c_j \sim p(c)\)。注意到,这样给出的观测值变为2维的(包括 $\tau_{j}$ 和 $w_{j}$)。
节奏分析
节拍图
A. T. Cemgil, H. Kappen, P. Desain, and H. Honing. On tempo tracking: Tempogram Representation and Kalman filtering. Journal of New Music Research, 28:4:259–273, 2001.
为了从局部的起始点序列 $ \mathrm{t} = [t_i]$ 中推断出节拍轨 $(\tau,\Delta)$,定义一个贝叶斯概率模型
\[p(\tau,\Delta,\mid \mathrm{t}) \propto p( \mathrm{t}\mid \tau,\Delta)p(\tau,\Delta)\]其中 $ \mathrm{t} = [t_i]$ 是起始点序列,局部节拍 $\tau$ 和局部周期 $\Delta$ 由卡尔曼滤波器给出。公式的第一项 $p( \mathrm{t} \mid \tau,\Delta)$ 是似然函数,可以看成给定节拍轨 $(\tau,\Delta)$ 下观测到起始点序列 $t$ 的概率,第二项 $p(\tau,\Delta)$ 是节拍的先验分布。
一个合理的假设是当节拍轨 $(\tau,\Delta)$ 与观测序列 $[t_i]$ 匹配时,似然函数 $p( \mathrm{t} \mid \tau,\Delta)$ 较大,由此可以构造观测数据与局部节拍轨的相似性度量函数。
首先定义一个连续时域信号 \(x(t) = \sum_{i=1}^I G(t-t_i)\),其中 $G(t)$ 是一个方差为 $\sigma_x^2$ 的高斯函数 \(G(t)=\exp(-t^2 / 2\sigma_x^2)\) 。
局部节拍轨由一个脉冲序列 \(\phi(t;\tau,\Delta) = \sum_m \alpha_m \delta(t-\tau - m \Delta)\)表示,其中 \(\delta(t-t_0)\)是一个转换后的 Dirac delta 函数,表示位于 $t$ 处的脉冲。$\alpha_m$ 是脉冲的幅度,是一个正的常数,且满足 \(\sum_m \alpha_m = 1\)。 如果需要计算的因果性,可以在 $m > 0$ 限制 $\alpha_m = 0$ 。当 $\alpha_m$ 是指数响应序列,即 \(\alpha_m = \alpha_0^m\) 时,它变成无限脉冲响应(IIR)梳状滤波器。定义 $x(t)$ 在 $(\tau,\Delta)$ 处的节拍图(Tempogram)为 $x(t)$ 与脉冲序列的内积
\[\mathrm{Tg_x}(\tau,\Delta) = \int_{-\infty}^{\infty} x(t)\phi(t;\tau,\Delta)dt\]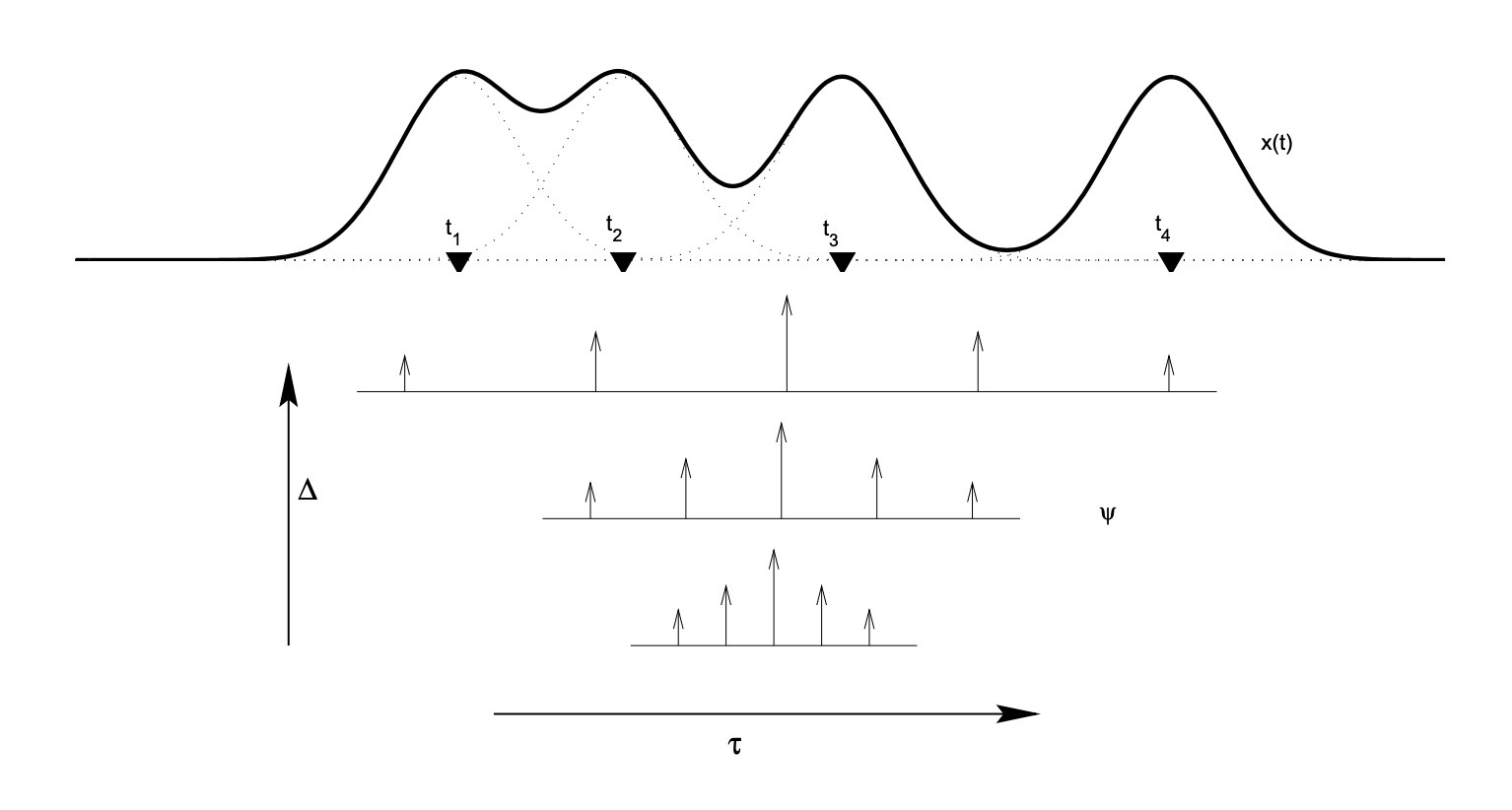
节拍图表示可以被解释为梳状滤波器组的响应,并且类似于多尺度表示(例如小波变换),其中 $\tau,\Delta$ 对应于转换和缩放参数。将似然函数定义为节拍图的对数
\[p( \mathrm{t}\mid \tau,\Delta) \propto \exp (\mathrm{Tg_x(\tau,\Delta)})\]假设 $\tau$ 和 $\Delta$ 的先验概率分布是平坦的,将 $\tau$ 边缘化得到 $\Delta$ 的概率分布
\[p(\Delta\mid \mathrm{t}) \propto \int \exp\left( \mathrm{Tg_x}(\tau,\Delta)\right) \mathrm{d} \tau\]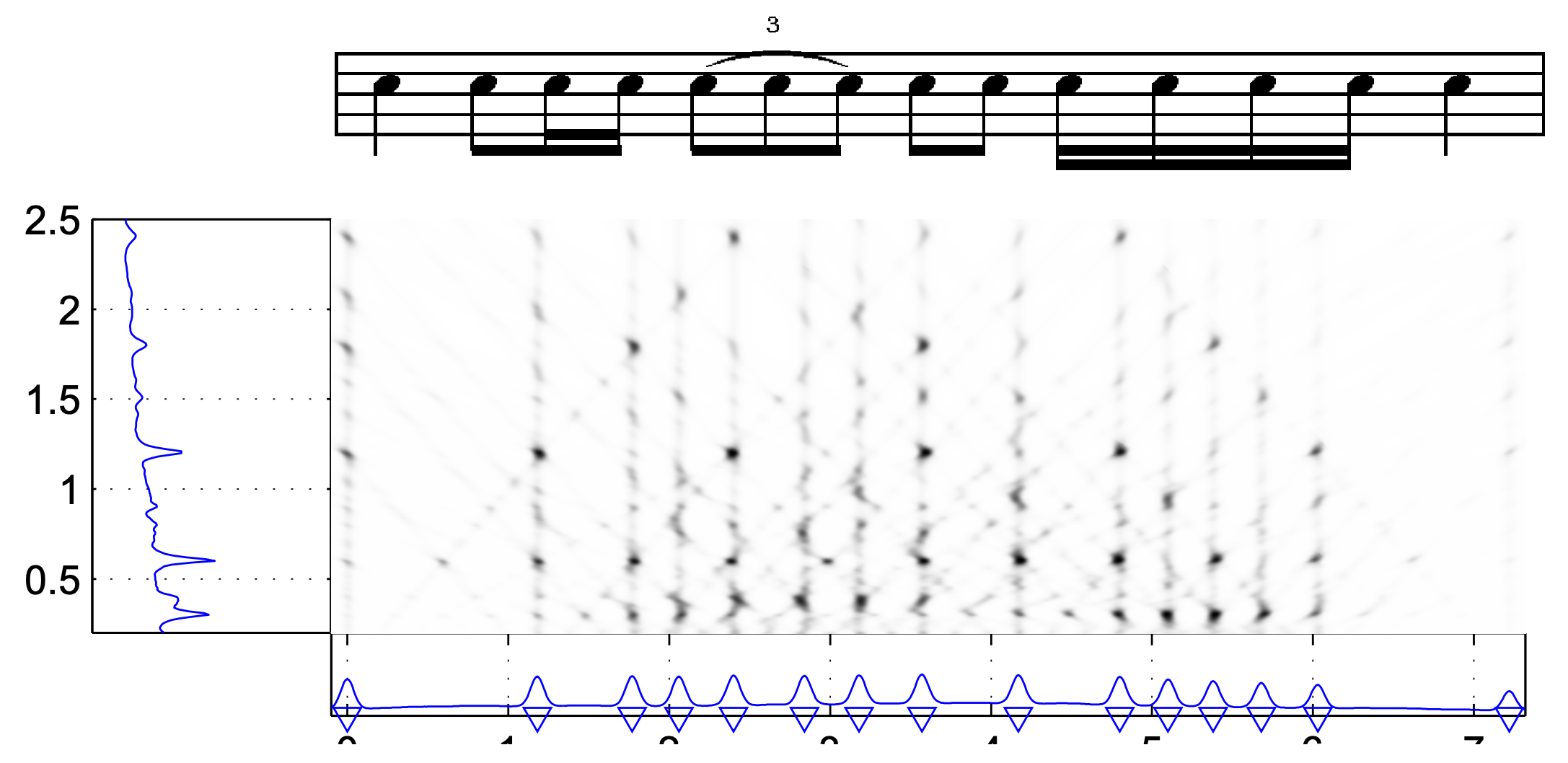
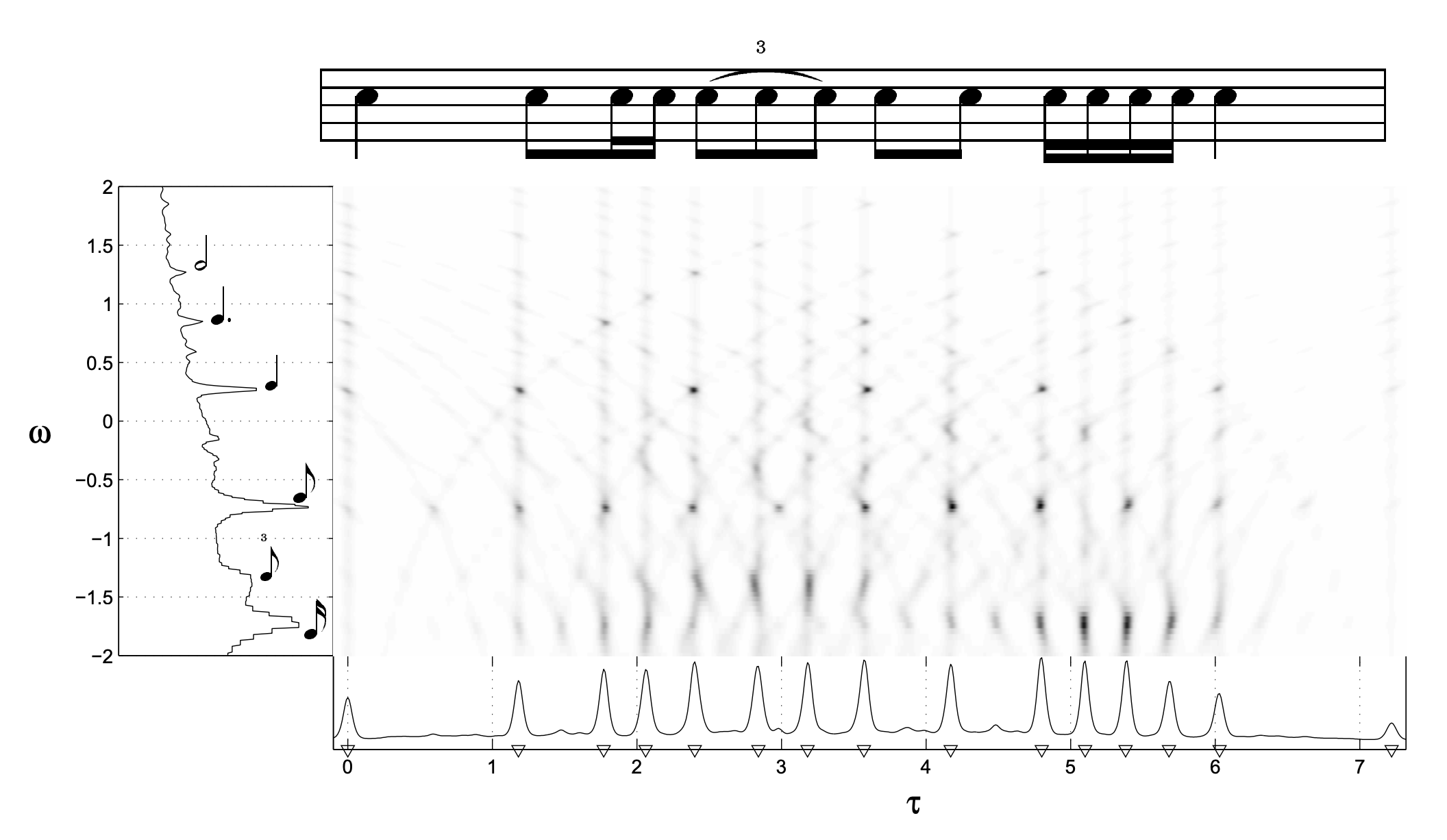
速度谱图
Grosche, Peter, Meinard Müller, and Frank Kurth. “Cyclic tempogram - A mid-level tempo representation for music signals.” ICASSP, 2010.
$\Delta$ 表示检测函数,长度为 6s 的 Hann 窗 $W$ 进行 STFT,对于频率 $\omega$,复数域的傅立叶系数 $\mathcal{F}(t,\omega)$ 定义为
\[\mathcal{F}(t,\omega) = \sum_{n\in \mathbb{Z}} \Delta(n)\cdot W(n-t)e^{-2\pi i\omega n}\]离散傅立叶速度谱图(Discrete Fourier Tempogram)定义为
\[\mathcal{T}^{F}(t,\tau) = \left|\mathcal{F}(t,\tau/60)\right|\]其中 $\tau$ 是 BPM,$\mathcal{T}^{F}(t,\tau)$ 表示在时刻 $t$ 时,以 $\tau$ BPM 进行的傅立叶变换的幅度。
保持窗宽 6s,检测函数的无偏局部自相关
\[\mathcal{A}(t,l) = \dfrac{\sum_{n\in \mathbb{Z}} \Delta(n)\Delta(n+l) \cdot W(n-t)}{2N + 1 -l}\]自相关速度谱图(Autocorrelation Tempogram)定义为
\[\mathcal{T}^{A}(t,\tau) = \mathcal{A}(t,l)\]其中,速度 $\tau = 60/(r\cdot l)$ BPM,$l \in [1:N]$ 是滞后,$r$ 对应于 STFT 步长。
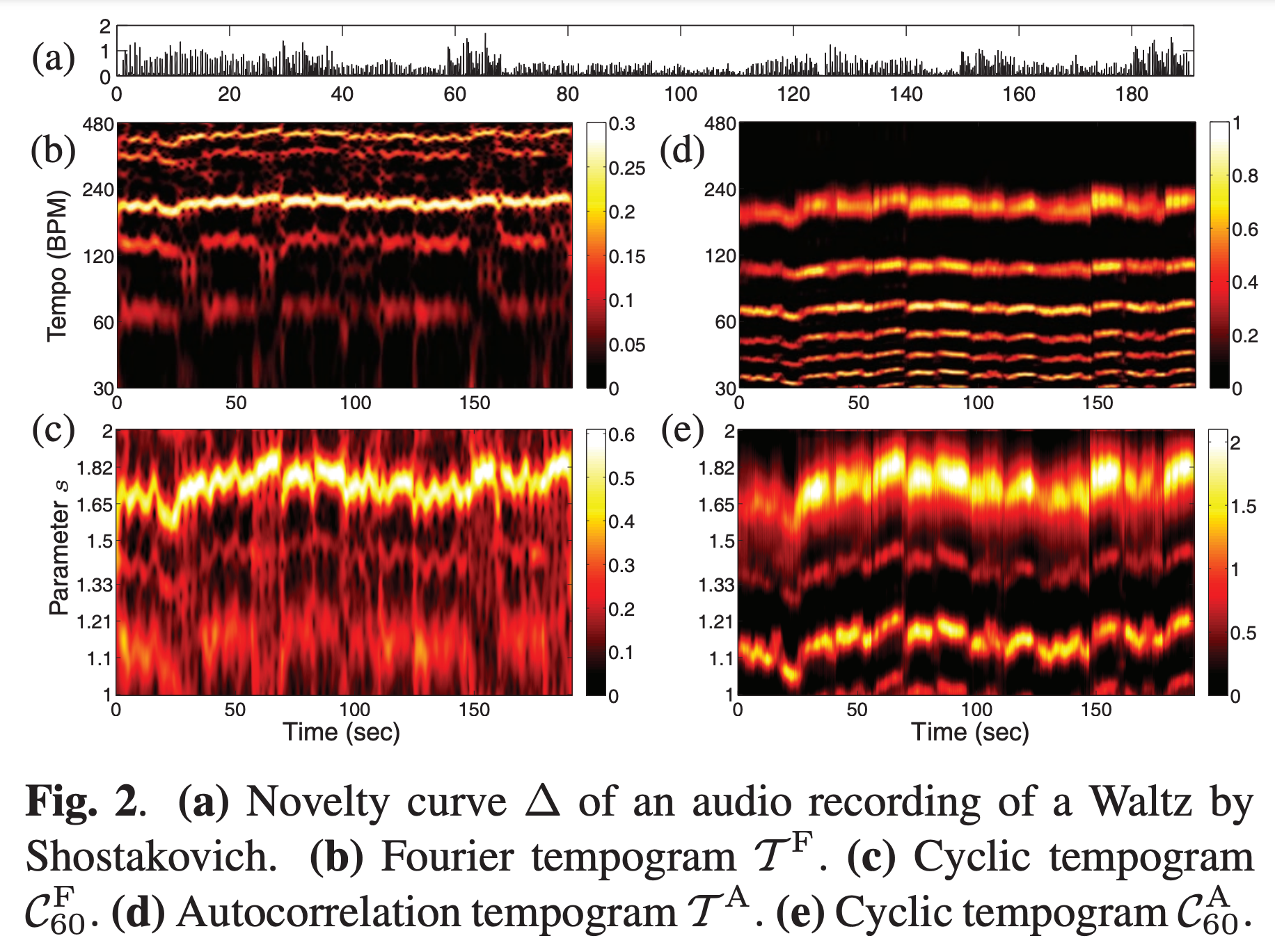
为了避免谐波的干扰,引入循环速度谱图(Cyclic Tempogram)
\[\mathcal{C}(t,[\tau])= \sum_{\lambda \in [\tau]} \mathcal{T}(t,\lambda)\]其中 $[\tau]$ 是 $\tau$ 的 $2^k$ 倍数的集合,例如对于 $\tau = 120$,\([\tau] = \left\{ \dots,30,60,120,240,480,\dots \right\}\)。
给定一个参考速度 $\rho$ BPM,循环速度谱图映射为 $\mathcal{C}_{\rho}$
\[\mathcal{C}_{\rho}(t,s)= \mathcal{C}(t,[\rho\cdot s])\]注意到 \(\mathcal{C}_{\rho}(t,s) = \mathcal{C}_{\rho}(t,2^k s)\),因此 $\mathcal{C}_{\rho}(t,s)$ 由因子 $s\in [1,2)$ 完全定义。
MATLAB 工具箱:TEMPOGRAM TOOLBOX
Grosche P, Müller M. Tempogram toolbox: Matlab implementations for tempo and pulse analysis of music recordings[C]//Proceedings of the 12th International Conference on Music Information Retrieval (ISMIR), Miami, FL, USA. 2011: 24-28.
流式速度估计
Percival, Graham, and George Tzanetakis. “Streamlined tempo estimation based on autocorrelation and cross-correlation with pulses.” IEEE/ACM Transactions on Audio, Speech, and Language Processing 22.12 (2014): 1765-1776.
Percival 等人提出一种针对音频流的实时速度估计算法,算法利用速度谱图(Tempogram)和累加器分步估计速度,用“广义自相关”和快速傅里叶变换加快自相关运算,在计算量和精度上取得不错的平衡。
起始点强度信号
1)分帧:将源音频(44100 Hz)按每帧 1024 个采样点、步长128 点分割,产生一系列采样率约为 344.5 Hz 的帧。
2)对数能量谱:每一帧都乘以汉宁窗,然后用离散傅里叶变换计算对数幅值谱 $L_P$。假设幅值谱用$|{X(k,n)}|$表示,那么
3)谱通量:对对数幅值谱所有具有正向差分的频率进行求和,得到谱通量。设 $N$ 是傅里叶变换得到离散频谱中正频率点的数量,这里 $N = 513$,计算中忽略离散频谱的直流分量(FFT 第 0 点)。$I_{PF}(k,n)$ 是一个指示函数,对频率谱对数幅度中的正差分进行选择。
\[\mathrm{Flux}(n) = \sum_{k=1}^{N-1}(L_P(k,n)-L_P(k,n-1)) \cdot I_{PF}(k,n)\]4)低通滤波:用 14 阶 FIR 滤波器对信号进行低通滤波,截止频率为 7 Hz ,汉明窗方法。
节拍周期检测
1)分帧:取 2048 个 $\mathrm{Flux}$ 帧 ( 2048 / 344.5 ≈ 6 s)进行分析,步长 128 点(128 / 344.5 ≈ 0.37 s)。假设总共会产生 M 个这种分析帧,采样率为 1 / 0.37 ≈ 2.7 Hz。
2)自相关:采用“广义自相关”,对于第 m 个分析帧,首先补零使帧长度加倍,然后计算其离散傅里叶变换,取压缩后的频谱幅值,然后进行离散傅里叶反变换:
\[A_m(t) = \text{IDFT}(|{\text{DFT}(\mathrm{Flux}(m))}|^c)\]其中 $c$ 控制了幅度的压缩度,$ c = 0.5 $ 能较好平衡自相关分辨率和对噪声的敏感度。
3)增强谐波:增强自相关 $EAC$ 由 $A_m$ 和其自身的 2 倍和 4 倍拉伸相加构成:
\[{EAC}_m(t) = A_m(t) + A_m(2\cdot t) + A_m(4 \cdot t)\]4)峰值提取:提取 $EAC$ 中最高的 10 个峰,舍弃 50 ~ 210 BPM 之外的候选速度,即保留滞后在 98 ~ 414 点之间峰的集合 ${P}$。
5)评估脉冲序列:给定一个候选自相关滞后 $P$ 和候选相位 $\phi$ (节拍出现的时刻),用参数 $v = 1,\ 1.5,\ 2$ 来生成三个脉冲序列:
\[I_{P,\phi,v} = \phi+vBP \quad B = 0,1,2,3\]三个序列按照 1.0 : 0.5 : 0.5 加权求和,变成单一的脉冲序列 $I_{P,\phi}$,索引超过 $\mathrm{Flux}$ 帧长度的脉冲忽略,然后与 $\mathrm{Flux}$ 做互相关运算
考虑所有可能的相位 $\phi$,定义
\[\rho_P(\phi,m) = \mathrm{Flux}(m) \star I_{P,\phi} \quad \phi = 0,1,...(P-1)\]然后计算两个评分函数:关于相位的自相关函数中最大的值 $SC_x$ ,和它们的方差 $SC_v$
\[SC_v(P,m) = \mathrm{var}_{\phi}(\rho_P(\phi,m))\\ SC_x(P,m) = \mathrm{max}_{\phi}(\rho_P(\phi,m))\]这两个评分归一化后相加得到第 m 帧的候选速度 P 的最终得分:
\[SC(P,m) = \frac{SC_x(P,m)}{\sum_c SC_x(P,m)} + \frac{SC_v(P,m)}{\sum_c SC_v(P,m)}\]最高评分的候选速度作为第 m 帧的速度
\[L_{\text{local}}(m) = \arg \max SC(P,m)\]高斯化累加:根据第 m 帧局部主导速度生成一个高斯曲线 $G(m)$,对于不同的 $L_{\text{local}}(m)$,使用固定的 $\sigma=10$ 会在 BPM 域中产生不同的的速度估计范围,速度越快,对应的范围越宽。
\[G(m) = \frac{1}{\sigma\sqrt{2\pi}} \exp\{-\frac{[x-L_{\mathrm{local}}(m)]^2}{2\sigma^2}\}\]每一帧产生的 $G(m)$ 都被累加到一个累加器 $C$ 中,$C$ 是足够容纳所有可能自相关滞后的向量。对历史数据使用指数衰减予以削弱,通过系数 $\alpha$ 来调节历史数据的衰减速度和新数据的累加速度,$\alpha$ 取 0.97。
\[C(m) = \alpha \cdot C(m-1) + (1-\alpha) \cdot G(m)\]峰值提取:从 $C$ 中选取最高的峰,得到当前时刻最佳估计速度
\[L(m) = \arg \max C(m)\] \[\Delta_{I} =\frac{L(m)}{F_s}, \quad \text{BPM} = \frac{60\cdot F_s}{L(m)},\quad F_s ≈ 344.5 \mathrm{Hz}\]动态规划
Ellis, Daniel PW. “Beat tracking by dynamic programming.” Journal of New Music Research 36.1 (2007): 51-60.
目标函数定义为节拍点检测函数的值O求和,加节拍间距定义的惩罚项F
\[C = \sum_{i=1}^{N} O(t_i) + \alpha \sum_{i=2}^{N}F(t_i - t_{i-1},\tau_p)\] \[F(\Delta t,\tau) = -\left( \log \frac{\Delta t}{\tau} \right)^2\]求极值点得到推断节拍序列 ${t_i} = \arg\max C $。 使用动态规划法,将目标函数分解为递推式:
\[C^*(t) = O(t) + \max_{\tau=0\dots t} \{\alpha F(t - \tau,\tau_p)+C^*(t)\}\]实际只搜索 $\tau=t-2\tau_p\dots t-\tau_p/2$,记录对应的极值点
\[P^*(t) = \arg \max \left\{ \alpha F(t-\tau,\tau_p) + C^*(\tau) \right\}\]找到最后一个极值点$t_N$之后,使用 $t_{N-1} = P^*(t_N)$ 回溯所有极值点。
隐马尔可夫模型
A. Klapuri, A. Eronen, and J. Astola. Analysis of the meter of acoustic musical signals. IEEE Transactions on Audio, Speech, and Language Processing, 14(1):342–355, January 2006.
N. Degara, E. Argones-R ́ ua, A. Pena, S. Torres-Guijarro, M. E. P. Davies, and M. D. Plumbley. Reliability-informed beat tracking of musical signals. IEEE Transactions on Audio, Speech and Language Processing, 20(1):290–301, January 2012.
G. Peeters and H. Papadopoulos. Simultaneous beat and downbeat-tracking using a probabilistic framework: Theory and large-scale evaluation. IEEE Transactions on Audio, Speech, and Language Processing, 19(6):1754–1769, 2011.
粒子滤波
S. Hainsworth and M. Macleod. Particle filtering applied to musical tempo tracking. EURASIP J. Appl. Signal Process., 15:2385–2395, January 2004. 8
Heydari, Mojtaba & Cwitkowitz, Frank & Duan, Zhiyao. (2021). BeatNet: CRNN and Particle Filtering for Online Joint Beat Downbeat and Meter Tracking.
动态贝叶斯网络
F. Krebs, S. B ̈ ock, and G. Widmer. Rhythmic pattern modeling for beat and downbeat tracking in musical audio. In Proceedings of the 14th International Society for Music Information Retrieval Conference (ISMIR 2013), pages 227–232, Curitiba, Brazil, November 2013.
MCMC
Cemgil A T, Kappen B. Monte Carlo Methods for Tempo Tracking and Rhythm Quantization[J]. Journal of Artificial Intelligence Research, 2003, 18: 45-81.
模型的结构等效于切换状态空间模型。开关变量与乐谱中的离散音符位置相对应。连续的隐藏变量表示节奏。比较了马尔可夫链蒙特卡罗(MCMC)方法(如吉布斯采样、模拟退火和迭代改进)和序列蒙特卡罗方法(粒子滤波器)。