概率分布的图形表⽰被称为概率图模型(Probabilistic Graphical Models)。这些模型提供了⼏个有⽤的性质:
- 它们提供了⼀种简单的⽅式将概率模型的结构可视化,可以⽤于设计新的模型。
- 通过观察图形,我们可以更深刻地认识模型的性质,包括条件独⽴性质。
- ⾼级模型的推断和学习过程中的复杂计算可以根据图计算表达,图隐式地承载了背后的数学表达式。
知识结构
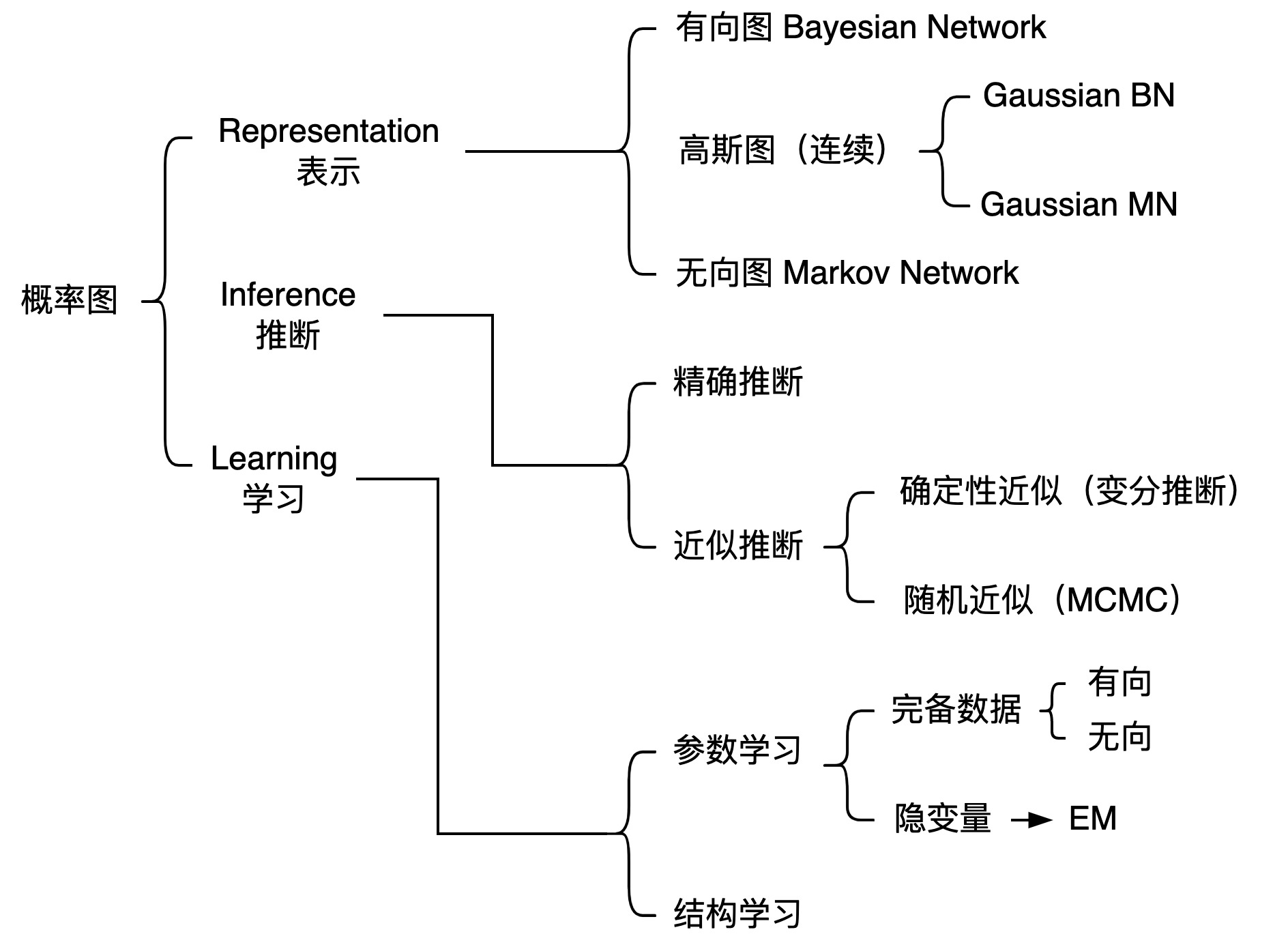
概率图模型基础
高维随机变量 $P(x_1,x_2,\dots,x_p)$:
- 边缘概率 $P(x_i)$
- 条件概率 $P(x_j\mid x_i)$
Sum Rule: $ P(x_1) = \int P(x_1,x_2)\mathrm{d} x_2 $
Product Rule: $P(x_1,x_2) = P(x_1) \cdot P(x_2\mid x_1) = P(x_2) \cdot P(x_1\mid x_2)$
Chain Rule: $P(x_1,x_2, \dots,x_p) = \displaystyle\prod_{i=1}^{p} P(x_i\mid x_1,x_2, \dots,x_{i-1})$
Bayesian Rule: $P(x_2\mid x_1) = \dfrac{P(x_1,x_2)}{P(x_1)}=\dfrac{P(x_1,x_2)}{\displaystyle\int P(x_1,x_2)\mathrm{d} x_2} = \dfrac{P(x_1,x_2)}{\displaystyle\int P(x_2) \cdot P(x_1\mid x_2)\mathrm{d} x_2} $
困境:维度高,求解复杂。$P(x_1,x_2, \dots,x_p)$ 计算量太大。
假设:互相独立
Naive Bayes:
\[P(x_1,x_2, \dots,x_p) = \prod_{i=1}^{P} P(x_i)\]假设: Markov Property
HMM (齐次 Markov 假设):
\[x_j \perp x_{i+1} \mid x_i, \quad j<i\]假设: 条件独立性
\[x_A \perp x_B \mid x_c,\quad x_A,x_B,x_C\ 是集合,且不相交\]贝叶斯网络 - 条件独立性
因子分解
\[P(x_1,x_2,\dots,x_p) = \prod_{i=1}^{p} P(x_i\mid x_{pa(i)})\]$ x_{pa(i)} $ 是 $ x_i $ 的父亲集合。
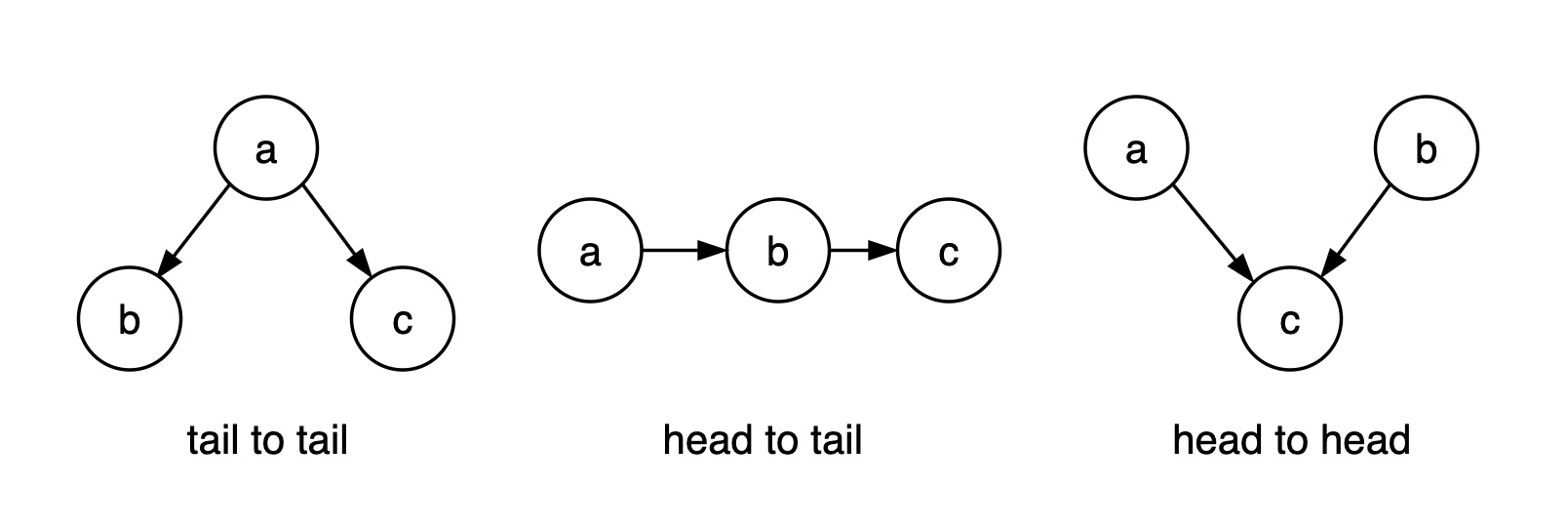
1. tail to tail
若a被观测,则路径被阻塞。
证明:
因子分解 $P(a,b,c) =P(a)P(b\mid a)P(c\mid a)$
链式法则 $P(a,b,c) =P(a)P(b\mid a)P(c\mid a,b)$
消元 $P(c\mid a) = P(c\mid a,b)$
由于 $P(c\mid a)\cdot P(b\mid a) = P(c\mid a,b)\cdot P(b\mid a) = P(b,c\mid a)$
推出 $P(c\mid a)\cdot P(b\mid a) = P(b,c\mid a)$,即 $c \perp b \mid a$。
2. tail to head
若b被观测,则路径被阻塞。
3. head to head
默认情况下,a $\perp$ b,路径是阻塞的,若 c(或其后继节点)被观测,则路径是通的。
head to head 比较费解,举例:
- a 酒量小
- b 心情不好
- c 喝醉
显然 $P(a) = P(a \mid b)$。已知小明喝醉的情况下酒量小的概率 $P(a\mid c)$,明显大于已知小明喝醉且心情不好的情况下,酒量小的概率 $P(a\mid b,c)$ ,即 $P(a\mid c) > P(a\mid b,c)$,说明 a 与 b 在给定 c 时不独立。
贝叶斯网络 - D-Seperation
\[P(x_i \mid x_{-i}) = \frac{P(x_i,x_{-i})}{P(x_{-i})} = \frac{P(x_i,x_{-i})}{\int_{x_i} P(x)\mathrm{d}x_i }=\frac{ \prod_{j=1}^{p}P(x_j\mid x_{pa(j)}) }{ \int_{x_i} \prod_{j=1}^{p}P(x_j\mid x_{pa(j)})\mathrm{d}x_i }\](马尔科夫毯)
贝叶斯网络 - 知识结构
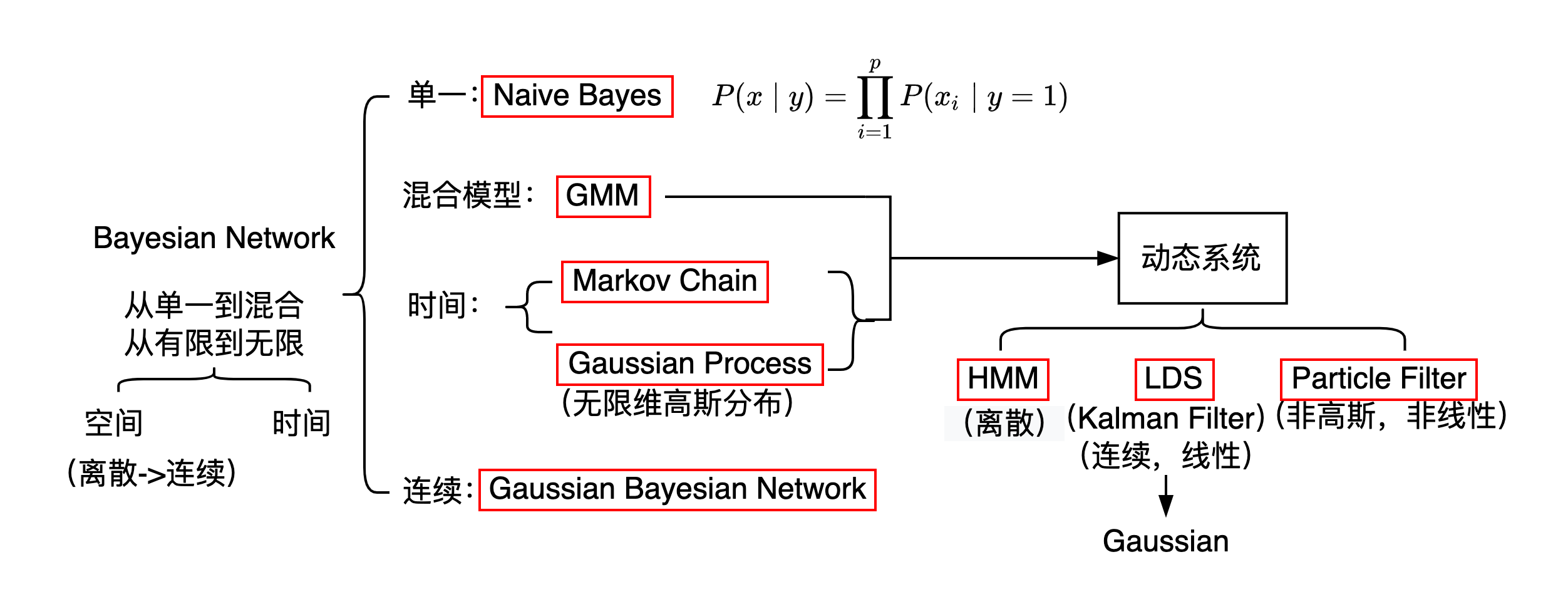
Markov Network(Markov Random Field 马尔可夫随机场)
条件独立性体现在三个方面:
$1$. Global Markov Property:如果 $A,B,C,$ 存在 $ \mathrm{Sep}(A,C\mid B)$,那么 $x_A \perp x_c \mid x_B$.
$2$. Local Markov Property:$x_i \perp {x_{-i-nb(i)}} \mid x_{nb(i)}$.
$3$. Pair Markov Property:$x_i \perp x_j \mid x_{-i-j},\quad x_i,x_j$ 没有边连接.
根据Hammesley-Clifford定理, 可得条件独立性的三种情况与基于最大团的因子分解等价 $1\Leftrightarrow 2\Leftrightarrow 3\Leftrightarrow $因子分解
团:一个关于节点的集合,集合中的节点之间相互都是连通的。
最大团:一个团内不能再添加节点的团。
基于最大团的因子分解: \(P(x) = \frac{1}{Z} \prod_{i=1}^{K} \psi(x_{C_i})\) \(Z = \sum_{x_1,x_2,\dots,x_p} \prod_{i=1}^{K} \psi(x_{c_i})\)
$C_1,C_2,\dots,C_K$: K个最大团
$x_{C_i}$: 最大团随机变量的集合
$Z$: 归一化因子
$\psi(x_{C_i})$: 势函数,必须为正
$P(x)$ 称为 Gibbs Distribution (Boltzmann Distribution),
\[P(x) = \dfrac{1}{Z} \prod_{i=1}^{K} \psi(x_{C_i}) = \dfrac{1}{Z} \prod_{i=1}^{K} \exp{\{-E(x_{C_i})\}} = \dfrac{1}{Z}\exp{\{-\sum_{i=1}^{K}E(x_{C_i})\}}\]形式上为指数族分布
\[P(x)=h(x)\exp\{\eta^T\phi(x)-A(\eta)\}={1\over Z(\eta)}h(x)\exp\{\eta^T\phi(x)\}\]Markov Random Field $\Leftrightarrow$ Gibbs Distribution,证明略。
Inference - 知识结构
Tasks: 给定 $P(x) = P(x_1,x_2,\dots,x_p)$ 求:
$1.$边缘概率: $P(x_i) = \displaystyle\sum_{x_1}\dots\sum_{x_{i-1}}\sum_{x_{i+1}}\dots\sum_{x_p}P(x)$;
$2.$条件概率(后验概率):$P(x_A\mid x_B),\quad x = x_A \cup x_B$;
$3.$最大后验 MAP: $\hat{z} = \displaystyle \arg\max_{z} P(z\mid x) \propto \arg\max_{z} P(z,x)$ ;
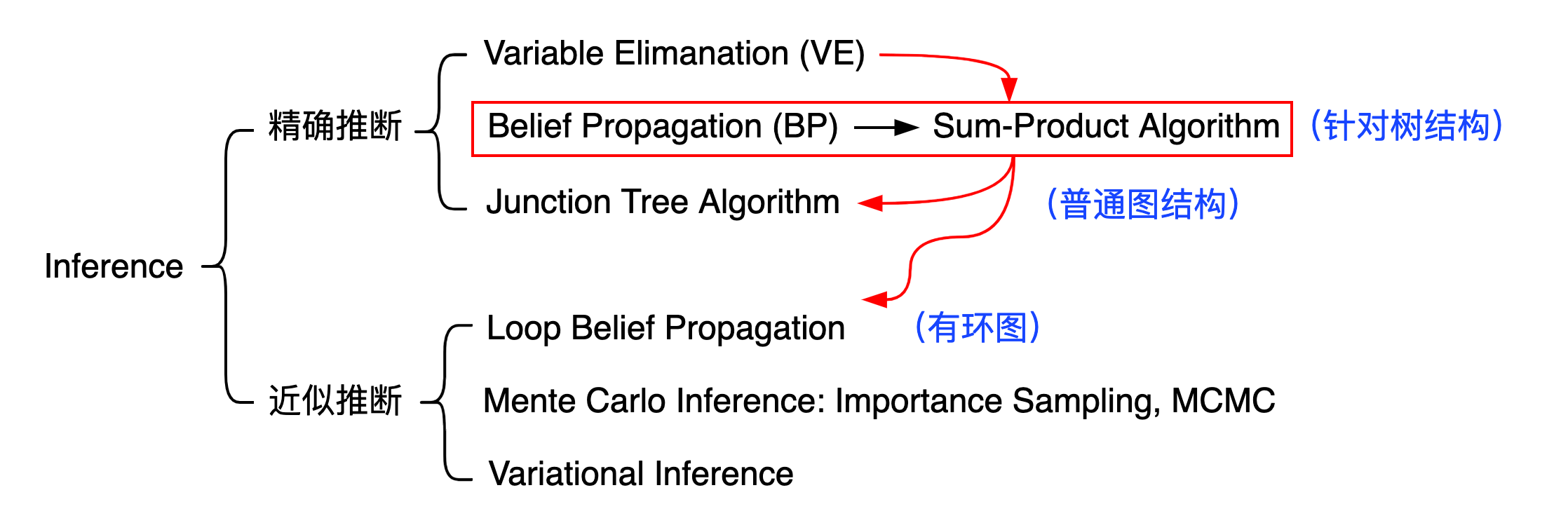
HMM Inference 中的三个问题:
$1.$ Evalution 边际化: $P(O) = \sum_{I} P(I,O) \Rightarrow$ 解决方法:前向、后向;
$2.$ Learning: $\hat{\lambda}$;
$3.$ Decoding: $\tilde{I} = \arg\max_{I} P(I\mid O)$ $\Rightarrow$ Viterbi Algorithm(动态规划).
HMM $\Rightarrow$ Dynamic Bayesian Network
Inference - Variable Elimination 变分推断

(VE的核心思想:乘法分配律) \(\begin{split} p(d)&=\sum_{a,b,c} p(a)p(b\mid a)p(c\mid b)p(d\mid c)\\ &=\sum_{b,c}p(c\mid b)p(d\mid c)\sum_{a} p(a)p(b\mid a)\\ &=\sum_{b,c}p(c\mid b)p(d\mid c)\underbrace{\sum_{a} p(a,b)}_{\phi_a(b)}\\ &=\sum_{c}p(d\mid c)\underbrace{\sum_{b}p(c\mid b)\phi_a(b)}_{\phi_b(c)}\\ &=\phi_c(d) \end{split}\)
推广到无向图,使用最大团分解,$K$ 是最大团的个数:
\[P(a,b,c,d) = \dfrac{1}{Z}\prod_{i=1}^{K}\phi_{C_i}(x_{Ci})\]由于是最大团,不能再添加其他结点,因此团与团的联系较小,同时每一个结点几乎不可能同时存在于所有团,因此同样可以使用Variable Elimination方法进行计算。
VE算法的局限性:
- 上述例子只计算了结点 d ,若需要计算其他结点,又要重新计算,每次计算的中间结果没有存储,导致重复计算。
- 变量消除的次序会决定时间复杂度,已被证明找到最优次序是一个NP-Hard问题,因此也可以使用一些启发式思想进行次序选择。
Inference-Belief Propagation
以5节点链 a->b->c->d->e 为例,先进行因子分解:
\[P(a,b,c,d,e)=P(a)P(b\mid a)P(c\mid b)P(d\mid c)P(e\mid d)\] \[\begin{split} P(e)&=\sum_{a,b,c,d} P(a,b,c,d,e)\\ &=\sum_dP(e\mid d)\sum_cP(d\mid c)\sum_bP(c\mid b)\sum_aP(b\mid a)P(a)\\ &=\sum_dP(e\mid d)\sum_cP(d\mid c)\sum_bP(c\mid b) \color{red}{m_{a\to b}(b)}\\ &=\sum_dP(e\mid d)\sum_cP(d\mid c) \color{red}{m_{b\to c}(c)}\\ &=\sum_dP(e\mid d) \color{red}{m_{c\to d}(d)}\\ &= \color{red}{m_{d\to e}(e)}\\ \end{split}\]上述是一个前向传播过程(Forward Algorithm),类似于HMM的过程。
若我们需要求 $P(c)$ ,则:
\[P(c)=(\sum_{b}P(c\mid b)\sum_aP(b\mid a)P(a))\cdot(\sum_{d}P(d\mid c)\sum_eP(e\mid d))\]先从 a 到 b , 再从 e 到 d ,先前向传播,再反向传播(Forward-Backward Algorithm) 其中前向传播的计算与求 $P(e)$ 的部分计算一样,重复计算。
从这个例子可以看出上节讲的VE算法的缺点:重复计算。
本节引入Belief Propagation算法,其基本思想与VE一致
不同的是:将中间过程存储起来,简化计算,避免重复计算。
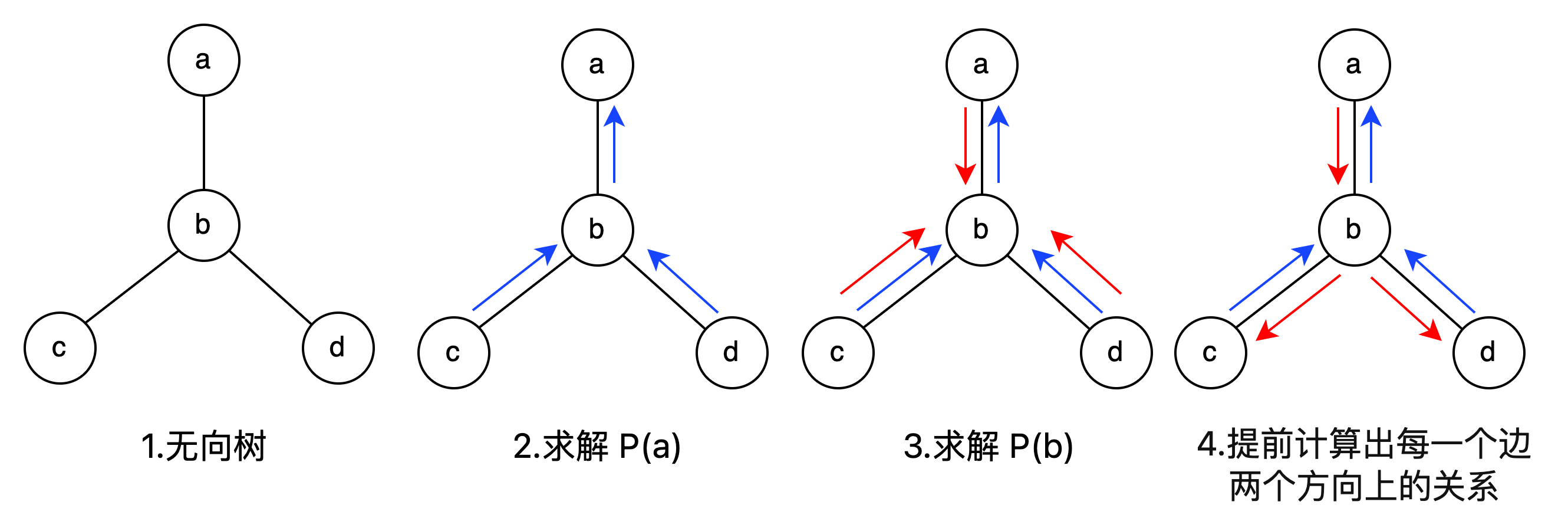
以 P(a) 为例:
\[\begin{split} P(a)&=\sum_{b,c,d}P(a,b,c,d)\\ &=\psi_a\sum_b((\sum_c\psi_c\psi_{b,c})\cdot \psi_b\cdot(\sum_d\psi_d\psi_{b,d})\cdot \psi_{ab})\\ &=\psi_a\sum_b(m_{c\to b}(b)\cdot \psi_b\cdot m_{d\to b}(b)\cdot \psi_{ab})\\ &=\psi_a m_{b\to a}(a) \end{split}\]此式共有两个部分:
\[\begin{cases} m_{b \to a}(a)=\displaystyle\sum_b \psi_{a,b} \psi_b m_{c\to b}(b)m_{d\to b}(b)\\ P(a)=\psi_a m_{b \to a}(a) \end{cases}\]进行简化( $NB(b)$ 为 b 结点的邻居结点所组成的集合):
\[\begin{cases} m_{b \to a}(a)=\displaystyle\sum_b \psi_{a,b} \psi_b \prod_{k\in NB(b)}m_{k \to b}(b)\\ P(a)=\psi_a m_{b \to a}(a) \end{cases}\]再进行归纳(generalize),得到边缘概率的递推公式:
\[\begin{cases} m_{j \to i}(i)=\displaystyle\sum_j \psi_{i,j} \cdot \underbrace{\psi_j \prod_{k\in NB(j)}m_{k \to j}(j)}_{\mathrm{Belief}(j)}\\ P(i)=\psi_i \displaystyle\prod _{k\in NB(i)}\underbrace{m_{k \to i}(i) }_{j\mathrm{的Children}}\end{cases}\]-
$\displaystyle\psi_j \prod_{k\in NB(j)}m_{k \to j}(j)$ 称为 $\mathrm{Belief}(j)$
-
$ m_{k \to j}$ 称为 $j$ 的Child.
根据避免重复计算的思路,可得出结论:
不要直接求边缘概率 $(P(a),P(b),\cdots)$ ,只需求 $m_{i\to j}$
相当于做了一个cach,存储中间结果
算法流程:
Belief Propagation (Sequential Implementation)
- Get Root, assume a is root
- Collect Message (求 $m_{x_i \to \mathrm{Root}}$)
for x_i in NB(Root): collectMsg(x_i) - Distribute Message (求 $m_{\mathrm{Root} \to x_j}$)
for x_j in NB(Root): distribute(x_j)
可得 $m_{ij}$ for all $i,j\in$ 节点集合 $V$ 从而 $P(x_k), k\in V$
Belief Propagation (Parellel Implementation)
- 随机找一个点 x
- 求信息量 (刚开始只有 $\psi _x$)
- 向他的邻居结点发生通知
- 邻居结点收到通知后进行同样的操作
- 然后将消息传递回去
最终会收敛,求得所有的 $m_{i \to j}$
Inference-Max Product
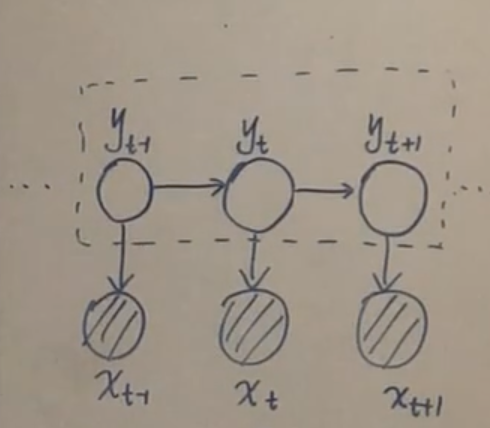
Decoding: $\displaystyle \hat{Y}=\arg\max_{Y} P(Y\mid X)$. 具体的算法:Viterbi,实际上是动态规划问题。
Max-product: BP 的改进,Viterbi 的推广。
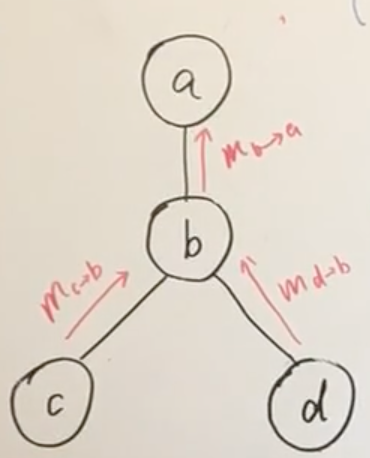
图中 $m_{c \to b}$ 表示能使得 c 结点概率最大的值, $m_{d \to b}$ 同理
$m_{b \to a}$ 表示能使得 c,b,d 联合概率最大的值
因此传递到结点 a 后,便是能使得 P(a,b,c,d) 最大的值
\[(x_a^*,x_b^*,x_c^*,x_d^*)=arg\underset{x_a,x_b,x_c,x_d}{max}P(x_a,x_b,x_c,x_d\mid E)\]在BP算法中: $m_{j\to i}(i)=\sum_j \psi_{i,j} \psi_j \prod_{k\in NB(j)}m_{k \to j}(j)$
而在Max-Product算法中:
\[m_{j\to i}(i)=\underset{j}{\max} \psi_{i,j} \psi_j \prod_{k\in NB(j)}m_{k \to j}(j)\] \[m_{c\to b}=\underset{x_c}{\max} \psi_c \psi_{b,c}\]可以把 $\psi_c \psi_{b,c}$ 看作是一个关于 $x_c$ 的函数,也就是找到这个函数的最大值
\[m_{d\to b}=\underset{x_d}{\max} \psi_d \psi_{b,d}\] \[m_{b\to a}=\underset{x_b}{\max} \psi_b \psi_{a,b}\cdot m_{c \to b} m_{d \to b}\]$\psi_b \psi_{a,b}\cdot m_{c \to b} m_{d \to b}$ 是图中所有关于 $x_b$ 的函数 因此
\[\max P(x_a,x_b,x_c,x_d)=\underset{x_a}{\max}\psi_a\cdot m_{b\to a}\]最后自上到下返回就可求得最优时的状态序列 $x_a^,x_b^,x_c^,x_d^$
由此可以看出此算法与Vitebi算法如出一辙。
道德图(Moral Graph)
将有向图转为无向图
head-to-tail, tail-to-tail 将有向边替换为无向边,使用基于最大团的因子分解,和有向图的结果等价。head-to-head 则需要连接两个父节点。
总结为一个通用的规则:
- $\forall x_i \in G$ , 将 $\mathrm{parent}(x_i)$ 两两连接(将自己多个父节点【如果有】互相连接)
- 将有向边替换为无向边
在道德图上做划分等价于在原图上的D划分。
因子图(Factor Graph)
道德图可以将有向图转换为无向图,但是可能会引入环(head-to-head类型),可能变成图,但是之前讲的BP(Belief Propagation)算法只能在树上操作。
因此需要引入因子图(Factor Graph),此方法有两大出发点:
- 消去环
- 简便
因子图: $\displaystyle P(x)=\prod_s f_s(x_s)$
其中 $s$ 是图的节点子集, $x_s$ 是 $x$ 的随机变量子集
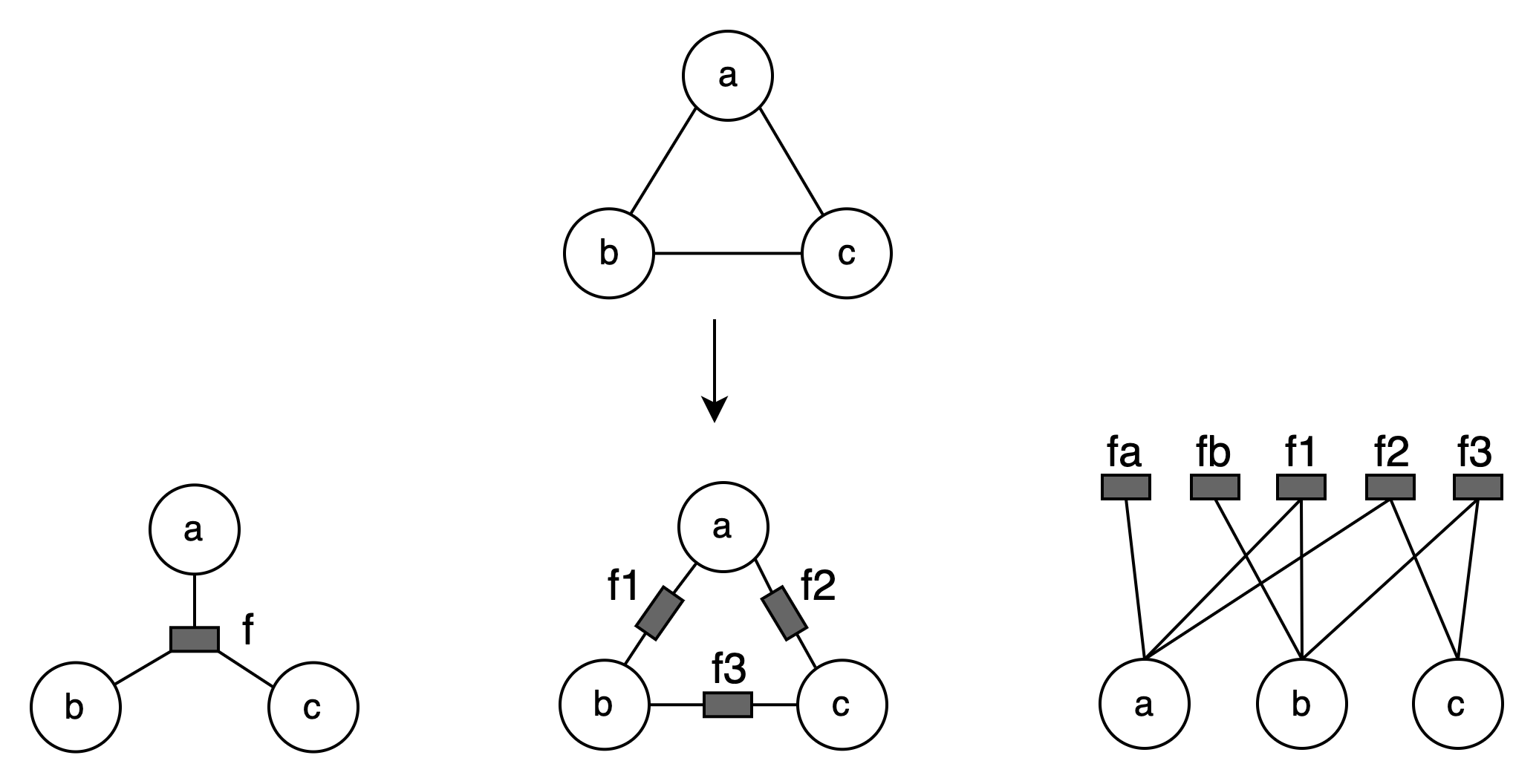
$f=f(a,b,c)$, $P(x)=f_1(a,b)f_2(a,c)f_3(b,c)$, 还可以更细的分解,如 $f_a(a),f_b(b)$
因子图:看作是对因式分解的进一步分解
在因子图中,原节点之间不再有联系。
每一种因子图都可以使用这种两层结构来表示。